補碼格式數據在民機試飛數據處理中的應用
通過線性方程進行分析,修改點對校準曲線,可以解決這個問題。修改點對校準曲線的方法是,將碼值為非負整數的特征點保持不便,把碼值為負整數的特征點換算成補碼,然后將補碼按照無符號值和原碼值對應,構成新的點對校準曲線,按照補碼的單調性和直線的平移性可知,這種方式的變換不改變計算的結果。本文引用地址:http://www.104case.com/article/192746.htm
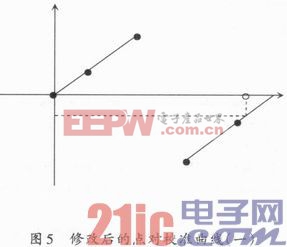
轉換后的點對校準曲線如圖5所示,按照這種方式就能求解出正確的物理量。但是,還有一種特殊情況沒有考慮到,如果僅僅按照轉化點對校準曲線的方法來處理補碼數據,對于大于x2又小于32 767的值,將會出現錯誤,如圖6所示。
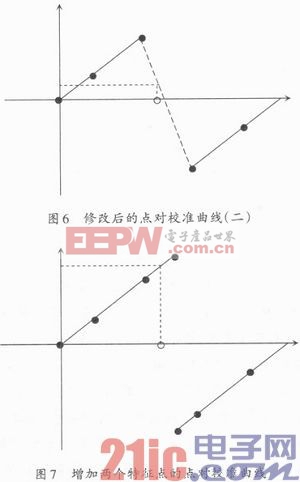
從圖6中可以看出,對于大于x2小于x3的碼值,經過上述方法進行處理,將得到錯誤的物理量。通過增加點對校準曲線的特征點可以解決這種特殊情況。在特征點x2和x3之間加入兩個新的特征點x2’=32 767和x3’=32 768,并按照線性外插分別求出x2’對應的物理量y2’和x3’對應的物理量y3’,如圖7所示。
由圖7可知,能正確解算圖6出現的特殊情況。
4 結語
本文通過討論校準曲線和試飛數據處理方法的關系,以及補碼在數值上單調性,采用解析幾何中線性方程平移的特性。提出了僅對校準曲線做一定的修改,就能正確處理補碼格式的試飛數據。這種解決方法不用修改標準化的試飛數據處理軟件,就能得到正確的試飛數據處理結果,有效地保障了支線飛機定型試飛任務的順利進行。同時,也給生成校準曲線的試飛工程師提供了一種解決類似問題的思路。









評論