基于FPGA的高階全數字鎖相環的設計與實現

　　鎖相環在通信、雷達、測量和自動化控制等領域應用極為廣泛，已經成為各種電子設備中必不可少的基本部件。隨著電子技術向數字化方向發展，需要采用數字方式實現信號的鎖相處理。因此，對全數字鎖相環的研究和應用得到了越來越多的關注。

　　傳統的數字鎖相環系統是希望通過采用具有低通特性的環路濾波器，獲得穩定的振蕩控制數據。對于高階全數字鎖相環，其數字濾波器常常采用基于DSP 的運算電路。這種結構的鎖相環，當環路帶寬很窄時，環路濾波器的實現將需要很大的電路量，這給專用集成電路的應用和片上系統SOC（system on chip）的設計帶來一定困難。另一種類型的全數字鎖相環是采用脈沖序列低通濾波計數電路作為環路濾波器，如隨機徘徊序列濾波器、先N 后M 序列濾波器等。這些電路通過對鑒相模塊產生的相位誤差脈沖進行計數運算，獲得可控振蕩器模塊的振蕩控制參數。由于脈沖序列低通濾波計數方法是一個比較復雜的非線性處理過程，難以進行線性近似，因此，無法采用系統傳遞函數的分析方法確定鎖相環的設計參數。不能實現對高階數字鎖相環性能指標的解藕控制和分析，無法滿足較高的應用需求。

　　本文提出了一種基于比例積分（PI）控制算法的高階全數字鎖相環。給出了該鎖相系統的具體結構，建立了系統數學模型，并對其系統性能進行了理論分析。采用MATLAB 軟件對系統進行了仿真實驗。應用EDA 技術設計了該鎖相系統，并用FPGA 予以實現。

2 全數字鎖相環的結構及工作原理

　　基于比例積分控制算法的三階全數字鎖相環的系統結構如圖1 所示。該系統由數字鑒相器（DPD）、數字環路濾波器（DLF）和數控振蕩器（DCO）三個部件組成。

圖1 三階全數字鎖相環系統結構圖

　　本鎖相系統中由于數控振蕩器采用累加器的結構，因此，累加器輸出的并行碼就是數控振蕩器的輸出相位碼B，它反映了輸入信號和輸出信號之間的瞬時相位差。鑒相器中的寄存器是由一組D 觸發器構成。DCO 的輸出相位碼B 并行送到D 觸發器的D 端，在輸入信號的正向過零點對D 觸發器采樣，D 觸發器組的輸出E 就表示該采樣時刻的瞬時相位差，從而完成了數字鑒相功能。

　　數字環路濾波器的主要作用是抑制噪聲及高頻分量，并且控制著環路相位校正的速度與精度。為了提高鎖相系統的性能，設計了基于PI 控制算法的二階數字濾波器。其工作原理是對鑒相器輸出的相位誤差信號經一階積分環節、二階積分環節和比例環節調節后，分別產生積分控制參數NP1 和NP2，以及比例控制參數NI，然后取這三個控制參數之和作為數控振蕩器的控制參數。為使DLF 輸出的控制碼組在同一瞬間并行送入DCO，在這兩個環路部件之間接入一緩沖寄存器。

　　數控振蕩器是由全加器和寄存器構成的累加器組成。若累加器位長為N，則低位輸入端NL 接DLF的控制碼組G，高位NH 接DCO 自由振蕩頻率0 f 的控制碼組C（該參數可由設計者設定）。當控制碼組G 均為‘0’時，DCO 輸出端最高位AN 的輸出信號的頻率便是DCO 的自由振蕩頻率f0 。在環路鎖定過程中，控制碼組G 不是全為零，此時累加器的累加結果將進位而改變累加器的分頻系數，從而改變DCO 輸出信號的頻率，實現比例積分控制參數對本地估算信號的控制作用，最終達到鎖相的目的。

3 數字鎖相環系統性能的理論分析

3.1 鎖相環的系統結構

　　若采樣周期很短，并且把數字鑒相器、數字環路濾波器和數控振蕩器的增益系數歸并到環路總增益一起考慮，可畫出鎖相環在Z 域的系統結構如圖2 所示。

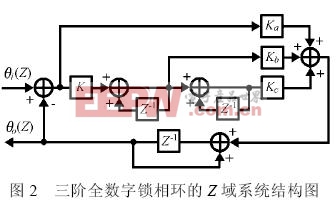
　　圖2 中θi(Z)為鎖相環的輸入信號；θo(Z)? 為鎖相環的輸出信號； K 為環路總增益； Ka 為比例環節系數； Kb 為一階積分環節系數； Kc 為二階積分環節系數。

　　由圖2 可以分別寫出該鎖相環開環、閉環和誤差Z 域傳遞函數：

3.2 鎖相環系統的穩態分析

3.2.1 系統的穩定性

　　由離散系統的奈奎斯特判據可知，環路系統穩定的充分必要條件是閉環傳遞函數的特征根必須全部位于Z 平面的單位圓內，只要有一個在單位圓外，系統就不穩定。由式（2）可得環路的特征方程為：

利用朱例（Jury）穩定判據，可以根據系統閉環特性方程的系數來判別特征根是否位于Z 平面的單位圓內，從而判別系統是否穩定。經分析推導可得，該三階數字鎖相環系統穩定的所有條件為：

3.2.2 系統跟蹤誤差

　　由系統誤差傳遞函數可以計算環路在各種不同輸入信號作用下的穩態跟蹤誤差，即：

θi(Z) 為輸入信號， He(Z) 為鎖相系統誤差傳遞函數。由式（6）所求得的本系統對應于各種典型相位輸入信號的穩態跟蹤誤差列于表1。
由表1 可知，本鎖相系統對于相位階躍、頻率階躍和頻率斜升輸入信號的穩態跟蹤誤差為零。

4 鎖相系統的設計實現與仿真

　　依據圖1 鎖相環系統的結構，利用Xilinx 公司的ISE 設計軟件，采用自頂向下的模塊化設計方法，用VHDL 對全數字鎖相環的各個部件分別進行編程設計，然后對該系統做綜合設計和仿真。最后，采用Xilinx 公司的sparnⅡ系列的FPGA 器件實現了鎖相系統的硬件功能。

　　本鎖相系統的設計參數如下：鑒相器中D 觸發器的位長為16；DLF 內二個積分環節中累加器的位長均為16；DCO 中累加器的位長為24，累加器的時鐘頻率fclk 為8MHz，比例積分控制碼組的字長G=14，自由振蕩頻率 f0 控制碼組的字長C=10。

　　選擇不同的比例系數Ka 和積分系數Kb 、Kc ，可以改變K1 、K2 、K3 的參數值，進而可根據本鎖相系統的穩定條件式（5），判斷系統是否穩定。表2 列出了幾種典型參數所對應的鎖相系統穩定性分析結果。

表2 中設

根據本系統在Z 域的傳遞函數和表2 中的設計參數K1 、K2 、K3 ，應用MATLAB 軟件進行分析，得到三階全數字鎖相環在單位階躍信號作用下的系統仿真曲線如圖3 所示。

從圖3 中系統仿真曲線可以看出，仿真實驗與理論分析的結果是一致的。調節比例和積分系數不僅能夠控制鎖相系統的穩定性，還可以控制系統的鎖相速度。顯然，在保持系統穩定的條件下，圖3(d)設計參數所對應的系統鎖相速度較快。

　　根據本系統在Z 域的誤差傳遞函數和實際設計參數，可以分別得到系統在相位階躍、頻率階躍和頻率斜升信號作用下的響應曲線如圖4 所示。從圖4 中可以看到，系統對于上述信號的穩態跟蹤誤差均為零。這與理論分析所得出的結論也是一致的。綜合考慮鎖相系統的穩定性、穩態相差和鎖相速度等性能指標， 最終選擇設計參數K1 = 2-3 ， K2 = 2-6， K3 = 2-11。

圖5 給出了采用EDA 技術設計的三階全數字鎖相環的系統仿真波形，圖中clkin 為系統時鐘信號，clr 為系統復位信號， ui 為輸入信號， uo 為輸出信號， uo1 為二倍頻輸出信號， uo2 為四倍頻輸出信號。從圖5 中可見，本鎖相系統可以同時得到倍頻輸出信號。

　　圖6 給出了用FPGA 實現的三階全數字鎖相環的硬件電路測試波形。系統仿真與硬件測試結果都表明，該系統能夠實現鎖相功能。

4 結論

　　本文提出了一種基于PI 控制算法的三階全數字鎖相環，采用EDA 技術進行系統設計，并用可編程邏輯器件予以實現。該鎖相環具有電路結構簡單、控制靈活、跟蹤精度高、環路性能好、易于集成的特點。在鎖相速度和穩定性方面優于已有的采用脈沖序列低通濾波計數方法實現的數字鎖相系統。理論分析和仿真實驗表明，改變比例積分控制參數，可以很方便地調節鎖相系統的鎖相速度和穩定性，因而簡化了設計過程。硬件測試結果證實，應用EDA 技術設計的高階全數字鎖相環能夠實現其鎖相功能。該鎖相環可作為功能模塊嵌入SoC 內，為各種控制系統提供快速、穩定和高精度的同步信號。