Widrow-Hoff神經網絡學習規則的應用研究
摘要:基于線性神經網絡原理,提出線性神經網絡的模型,并利用Matlab實現Widrow-Hoff神經網絡算法。分析Matlab人工神經網絡工具箱中有關線性神經網絡的工具函數,最后給出線性神經網絡在系統辨識中的實際應用。通過對線性神經網絡的訓練,進一步驗證Widrow-Hoff神經網絡算法的有效性,以及用其進行系統辨識的高精度擬合性。
關鍵詞:Widrow-Hoff學習規則;線性神經網絡;Matlab;系統辨識
1 引言
利用神經網絡解決實際問題時,必定涉及大量數值計算。為了解決數值計算與計算機仿真間的矛盾。美國MathWorks公司推出的集數學計算、圖形計算、語言設計、計算機仿真于一體的Matlab具有非線性適應性信息處理功能,克服傳統人工智能方法對于直覺,如模式、語言識別、非結構化信息處理方面的缺陷,使之在神經專家系統、模式識別、智能控制、組合優化、預測等領域獲得成功,具有極高的編程效率。神經網絡工具箱是以神經網絡理論為基礎,用Matlab語言構造的典型神經網絡工具函數。Matlab中大量有關線性神經網絡的工具函數可為線性神經網絡研究和應用提供強有力的工具。
2 線性神經網絡原理
2.1 線性神經網絡的模型
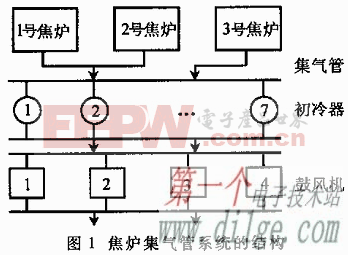
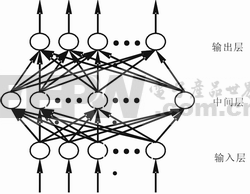
圖1是具有R個輸入的單層(有S個神經元)線性神經網絡結構,其權值矩陣為w,閾值向量為b,這種網絡也稱為Madaline網絡。
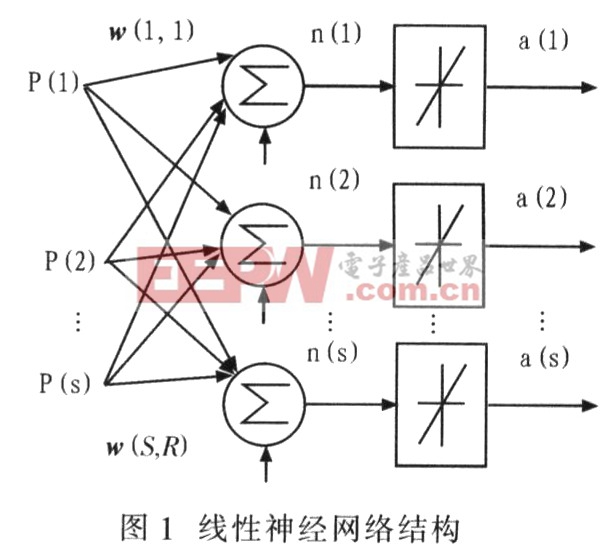
2.2 線性神經網絡的學習規則
線性神經網絡是基于線性神經網絡算法。線性神經網絡采用Widrow-Hoff學習規則,利用learnwh()函數修正網絡的權值和閾值。使用Widrow-Hoff學習規則訓練網絡某一層的權值和閾值,使其線性逼近一個函數式。
首先定義一個線性網絡的誤差函數:
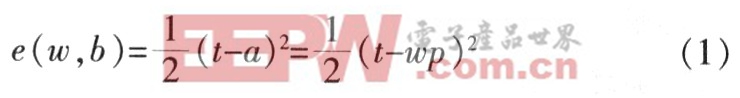
通過式(1)可知,線性網絡具有拋物面型的誤差曲面,因此只有一個誤差最小值。由于該值取決于網絡的權值和目標矢量,于是可通過調整權值使誤差達到最小。Widrow-Hoff學習規則是通過沿著相對于誤差平方和的最速下降方向,連續調整網絡的權值和閾值,根據梯度下降法,權值矢量的修正正比于當前位置上的e(w,b)的梯度,對于第i個輸出節點:
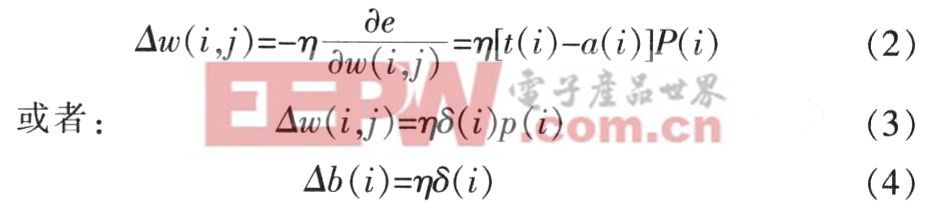
式中,η是學習率。
當η較大時,學習過程加速,網絡收斂較快,但η過大時,學習過程變得不穩定,且誤差增大;δ(i)=t(i)-a(i)。
以上各式為Widrow-Hoff學習規則最小均方誤差算法(LMS)。Widrow-Hoff學習規則的權值變化量正比于網絡的輸出誤差及網絡的輸入矢量。該算法無需求導,因此較簡單,并具有收斂速度快和精度高的優點。由于學習率與學習過程比較密切,因此學習率的取值非常關鍵。
采用Widrow-Hoff規則訓練的線性網絡,該網絡能夠收斂的必要條件是被訓練的輸入矢量必須是線性獨立的,且應適當選擇學習率。
3 線性神經網絡設計
Matlab神經網絡工具箱中含有易于構建的神經網絡函數。以下詳細說明線性神經網絡設計。
3.1 線性神經網絡的Matlab設計
3.1.1 線性神經網絡初始化
初始化是對連接權值和閾值進行初始化。initwb()初始化函數是對網絡的某一層的權值和閾值進行初始化,其格式為:net=initwb(net,i)。其中,i表示網絡的第i層。函數返回為第i層的權值和閾值都更新的網絡。
3.1.2 訓練網絡
線性神經網絡初始化后,就可對其訓練。設置參數,諸如學習步長、誤差目標等,同時在網絡訓練過程中,圖形顯示網絡誤差隨學習次數的變化而變化。
其格式為:
![]()
式中,Pd為延遲輸入;T為每一層的目標向量;Ai為初始輸入條件;Q為輸入向量個數;TS為時間步長;VV為空矩陣或確定的向量結構。
3.1.3 網絡仿真
仿真甬數sim()用來網絡仿真。其格式為:[Y,Pf,Af]=sim(net,{Q TS},Pi,Ai)。其中,Y為訓練好的線性神經網絡的實際輸出;Pf為最終輸出延遲;Af為最終的層延遲。
3.2 訓練步驟
(1)根據給定的輸入矢量計算網絡的輸出矢量a=wxp+b,并計算與期望輸出之間的誤差e=t-a;
(2)將網絡輸出誤差的平方和與期望誤差相比較,如果其值小于期望誤差,或訓練以達到事先設定的最大訓練次數,則終止訓練;否則,繼續訓練;
(3)采用Widfrow-Hoff學習規則計算新的權值和閾值,并返回至(1)。
4 線性神經網絡在系統辨識中的應用
4.1 工作原理
線性神經網絡用于線性系統辨識必須遵循系統辨識的3個基本構成原則:(1)選擇在滿足給定的誤差準則下逼近系統的最簡單模型;(2)輸入信號的頻譜必須足以覆蓋系統的頻譜;(3)誤差準則由誤差的泛函表示。
對于一個具有m個輸入和n個輸出的r階離散線性系統,可由n個差分方程來描述,其中第l個差分方程的一般形式表示為:
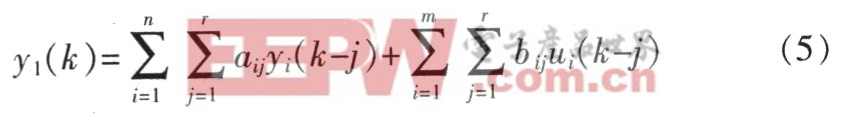
式中,aij和bij是方程右邊各項系數,如果某項系數為零,則該項與y1(k)無關,去掉該項。
從式(5)可以看出,線性系統k時刻的輸出可以由前面時刻有關輸入輸出線性表示,這種關系類似于單層線性神經網絡輸入輸出之間的關系。根據上述原則(1),建立線性神經網絡以辨識線性系統,神經網絡的輸入由系統輸入輸出信號的時延序列組成,網絡的輸入個數與系統階數有關,神經網絡的輸出代表系統輸出的估計值,網絡的輸出個數等于系統輸出個數。網絡建立后,根據基本構成原則(2),運用Widrow-Hoff學習規則訓練神經網絡,反復調節網絡的權值和閾值,使網絡輸出y(k)和系統輸出Y(k)之間的輸出誤差不斷減小,直至達到規定精度要求。
4.2 應用實例
設系統傳遞甬數為![]() 用線性神經網絡辨識其脈沖響應。設置如果迭代次數大于10 000或誤差小于0.001時,訓練結束。
用線性神經網絡辨識其脈沖響應。設置如果迭代次數大于10 000或誤差小于0.001時,訓練結束。
采用其工作原理及Widrow-Hoff規則訓練給定系統。訓練過程中,當迭代的次數大于10 000或誤差小于目標誤差時,訓練結束。圖2為訓練后的訓練誤差及步數曲線,由圖2看出,經過7 766步訓練后誤差達到0.000 999 252小于誤差目標e=0.001,訓練結束。
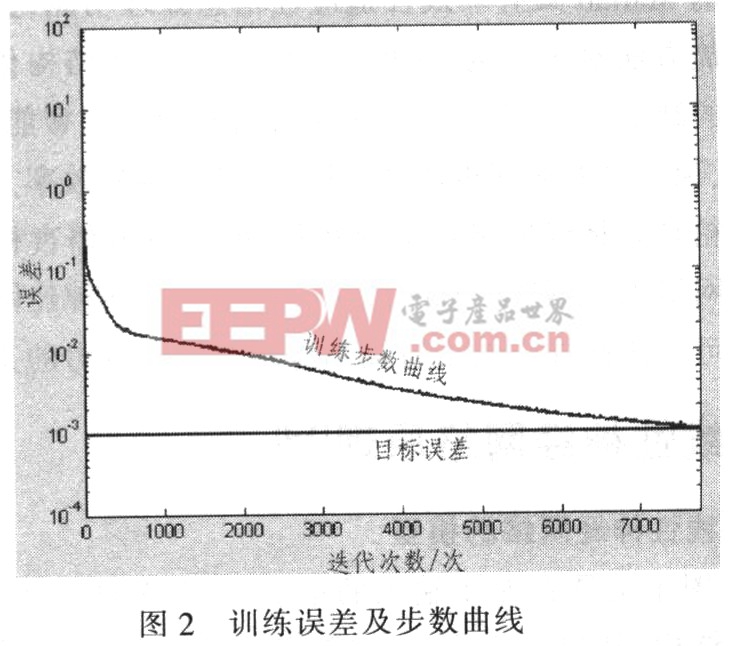
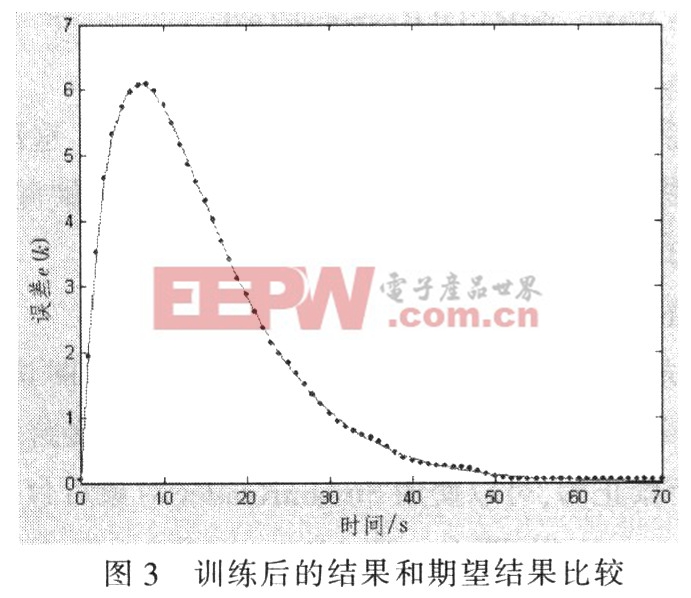
圖3為訓練后的結果與期望結果的比較,圖中,“?”表示訓練值,連續曲線表示理論值。由圖3可見,訓練值和理論值基本擬合。
需要注意的是,在訓練過程中發現,由于權值的初始值是隨機的,經多次訓練,每次的訓練結果都不一樣,有時訓練到10 000步時仍然收斂不到0.001。由此可見,初始權值的選取對訓練是有一定影響的。選取初始值時應要根據具體要求而定,不能隨意而定。
5 結語
論述的Widrow-Hoff學習規則算法可實現,仿真結果表明Widrow-Hoff學習規則無需求導,算法比較簡單,收斂速度快。采用線性神經網絡辨識系統,無需建立實際系統的辨識模式,因為線性神經網絡本身已作為一種辨識模型,可達到很高的辨識速度且擬合精度較高。該方法還可推廣至其他本質非線性系統。






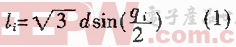

評論