基于FPGA的人工神經網絡實現方法的研究

(4)面積節省及相關問題
為了最小化神經元實現的面積，組成每個神經元的各個HDL算法模塊的面積也應該最小。乘法器以及基本的傳遞函數(例如，sigmoid激活函數tanh)是最占用面積的，這類問題非常依賴于所要求的精度，盡管神經網絡常并不要求很精確的計算，但是不同的應用所要求的精度不同。一般來講，浮點運算要比定點運算需要更大的面積，比如浮點運算中的并行加法器本質上是定點運算超前加法器加上必要的邏輯塊，減法器、乘法器也類似如此，這在激活函數實現方面更加突出，文獻[1]中面積優化對比顯示，32位浮點運算要比16位定點運算大250倍。另外，對于小型網絡，分布式存儲器很適合權值存放，但是對于大型網絡，權值存儲器不應該被放置在FPGA中，因此當ANN得到有效實現的時候，就要認真考慮存儲器的存取問題。其次，神經網絡應用有一個顯著的缺陷：在神經計算方面，不同運算的計算時間和實現面積并不平衡。在許多標準神經模式中，計算時間的大部分用在需要乘法器和加法器的矩陣向量運算中，而很多耗費面積的運算如激活函數，又必須被實現(它們占用很少的運算時間)，而FPGA的面積是嚴格一定的，因此可將面積的相當一部分用來實現這些運算，以至于FPGA僅剩的一小部分卻實現幾乎所有的運算時間。
(5)資源和計算速度的平衡(Trade-off)
對于FPGA，科學的設計目標應該是在滿足設計時序要求(包括對設計最高頻率的要求)的前提下，占用最少的芯片資源，或者在所規定的占用資源下，使設計的時序余量更大，頻率更高。這兩種目標充分體現了資源和速度的平衡思想。作為矛盾的兩個組成部分，資源和速度的地位是不一樣的。相比之下，滿足時序、工作頻率的要求更重要一些，當兩者沖突時，采用速度優先的準則。
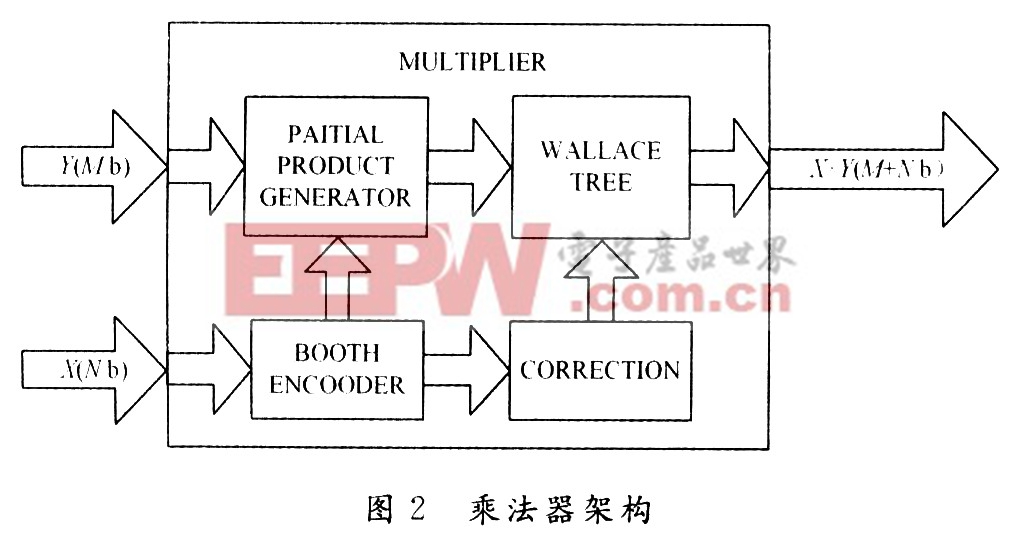
例如，ANN的FPGA實現需要各種字長的乘法器，如果可以提出一種新的運算法則，從而用FPGA實現變字長的乘法器，則可以根據需要調整字長，從而提高運算速度的可能性，其中，基于Booth Encoded opti-mized wallence tree架構(見圖2)就可以得到快速高效的乘法器，這種方式實現的乘法器比現在所用的基于FPGA的乘法器的處理速度快20％)。

(6)亟待解決的問題
FPGA憑借其如同軟件實現一樣的靈活性，集合了硬件實現高效和并行性的優點，好像非常適合神經實現的正常需要，但是，FPGA的二維拓撲結構不能處理標準神經網絡規則但復雜的連線問題，而且FPGA仍然實現很有限的邏輯門數目，相反，神經計算則需要相當耗費資源的模塊(激活函數，乘法器)。這樣對于FP-GA，可用的CLBs中部分將被用來增加路徑容量(連線)，導致計算資源的丟失。一般的方法只能實現很小的低精度神經網絡，連線問題不能依靠幾個具有比特序列算法的可重構FPGA以及小面積模塊(隨機比特流或者頻率)解決。

2 基于FPGA的ANN實現方法
經典實現方法有：
(1)可重構的RNN結構(Reconfigurable NeuraINetwork)
可重構計算是一種增加處理密度(每單元硅片面積的性能)的有效方法，且處理密度遠大于用于通用計算方法，FPGA作為可重構計算的平臺，可以提供如同軟件一樣的設計靈活性。該方法基于可擴展的脈動陣列結構、可重用的IP(Intellectual Properties)核及FPGA器件，即將要實現的神經網絡算法分為幾種基本運算，這些基本運算由可重構單元(Reconfigurable Cell，RC)完成，RC間以規則的方式相互連接，當神經網絡變化時，只要增減Rc的數量或替換不同功能的RC就可重構成新的神經網絡硬件；文獻[8]中同時指出，考慮到硬件實現要以最少的硬件資源滿足特定應用的性能需求，一般用神經元并行作為可重構部件的基本模式，即神經網絡的各層計算可復用相同的陣列結構。
(2)RENCO結構
可重構網絡計算機(Reconfigurable Network Computer，RENCO)是一種用于邏輯設計原型或可重構系統的平臺，所設計的可重構系統對于工作在比特級的算法實現特別有效，比如模式匹配。RENCO的基本架構包括處理器、可重構部分(多為FPGA)以及存儲器和總線部分，Altera公司提供的最新的RENCO在可重構部分包括近100萬邏輯門，足夠實現高復雜度的處理器。具體參見文獻[9]。盡管如此，得到的可重構系統并非對所有的硬件實現都是優化的方法，比如不適合于浮點運算。