基于陣列除法的數(shù)據(jù)接收／顯示模塊設(shè)計(jì)

對j=0

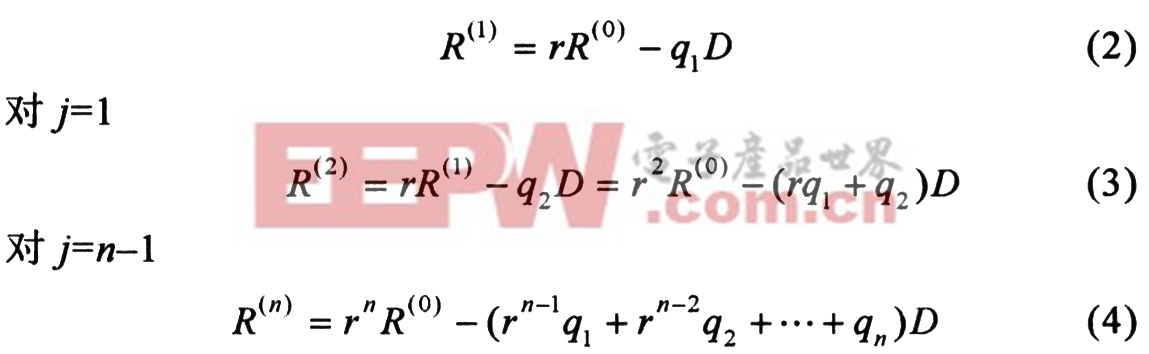
上述迭代推導(dǎo)過程說明了除法過程是由一系列加法、減法或移位所組成，對于基數(shù)r=2，q…∈{0，1}。
當(dāng)部分被除數(shù)rR(j)不夠除數(shù)D減時(shí)，商qj+1為0，同時(shí)補(bǔ)充被除數(shù)的下一位，組成更大的部分被除數(shù)；如果夠減，則該位商為1，在部分被除數(shù)rR(j)中減去除數(shù)D，然后補(bǔ)充被除數(shù)的下一位，直至被除數(shù)的每一位都使用到為止。
在除法進(jìn)行過程中，可使用專門的數(shù)據(jù)比較器來比較部分被除數(shù)rR(j)是否比除數(shù)D大(nonperforming算法)，或直接用部分被除數(shù)減去除數(shù)。方式1浪費(fèi)了專門的數(shù)據(jù)比較電路，運(yùn)算延遲加大，降低了運(yùn)算速度。方式2，當(dāng)完成了減法操作后，如果不夠減，把除數(shù)加回到產(chǎn)生的差，以恢復(fù)原來余數(shù)(恢復(fù)余數(shù)法)；或把產(chǎn)生的差留給下一次運(yùn)算時(shí)再處理(不恢復(fù)余數(shù)法)。

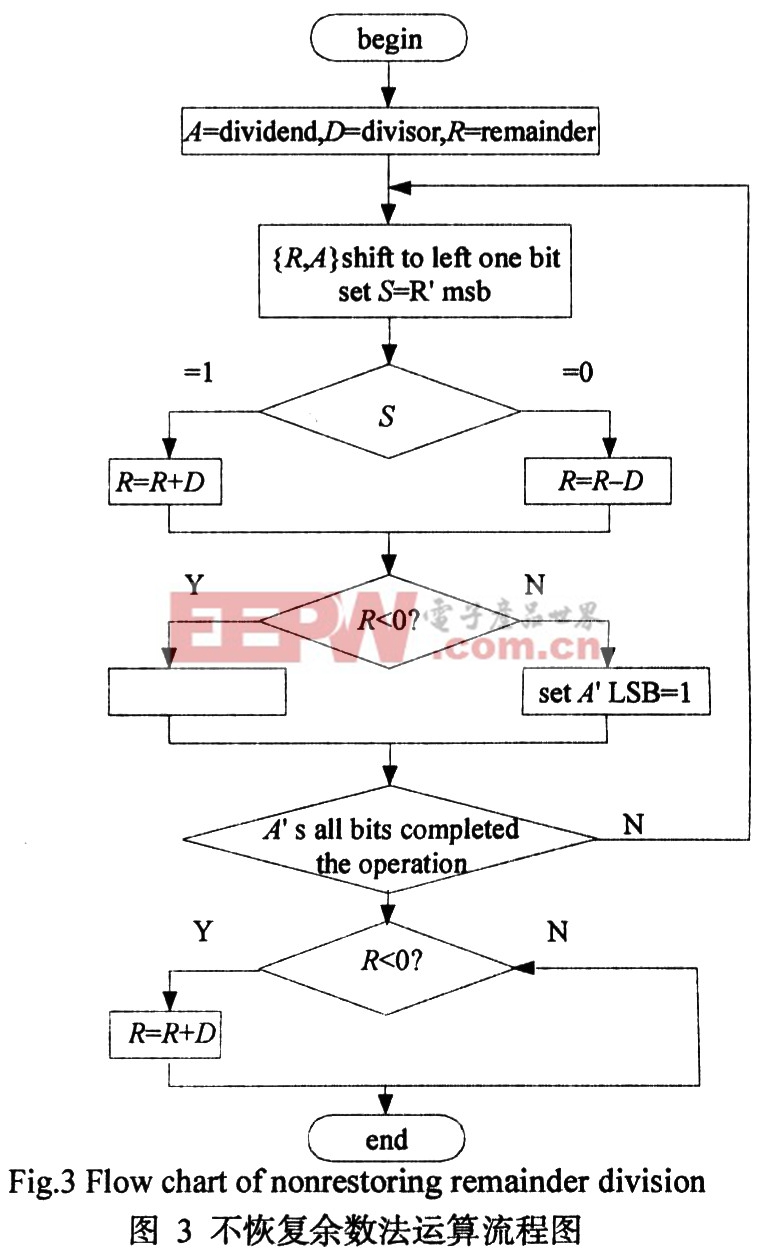
2．1 不恢復(fù)余數(shù)陣列除法器
為簡化起見，下文用A表示被除數(shù)，D表示除數(shù)，R表示余數(shù)。在恢復(fù)余數(shù)法中，如果余數(shù)R為負(fù)數(shù)，即不夠減，則需要加上除數(shù)D，恢復(fù)成原來的余數(shù)，即R+D。然后，余數(shù)R和被除數(shù)A聯(lián)合左移1位。此時(shí)余數(shù)為2(R+D)+ai，其中ai為A中的一位，被移入R中。隨后，進(jìn)入下一步運(yùn)算。即從余數(shù)中減去除數(shù)D：(2(R+D)+ai)-D，有
(2(R+D)+ai)-D=2R+ai+D (5)
因此，當(dāng)在某一步中，余數(shù)R為負(fù)，無需再加上除數(shù)D來恢復(fù)成原來的余數(shù)，只需在下一步中把恢復(fù)余數(shù)法中的減去除數(shù)D改成加上除數(shù)D，這種算法稱為不恢復(fù)余數(shù)法。恢復(fù)余數(shù)除法需要2個(gè)步驟來確定1個(gè)商位，而不恢復(fù)余數(shù)法沒有這個(gè)缺點(diǎn)。