廂式半掛車空氣懸架系統的Simulink仿真分析

一、動力學模型

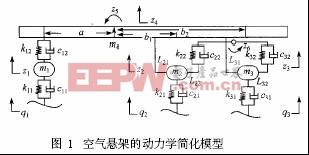
　　研究分析的對象為整個廂式半掛車的掛車部分，其副車架為雙軸。由于車身振動較小，忽略其橫向水平振動，而著重考察對平順性影響較大的垂直振動和縱向角振動。掛車簧下質量的振動是高頻振動，可以認為左右車輪的輸入是獨立的，不考慮其相互影響。假設廂式半掛車車輛左右對稱且左右輪的路面激勵相同，并作如下假設：（1）將車身視為具有集中質量的剛體；（2）牽引板與牽引座之間剛性連接，并用線性彈簧代替懸架，懸架剛度與阻尼分別是位移和速度的一次函數；（3）將牽引車后軸，副車架前后軸及車輪簡化為非簧載質量，用線性彈簧代替彈性輪胎，建立6自由度（用z1～z6表示）半掛車空氣彈簧動力學模型，q1、q2、q3 表示路面激勵，如圖1所示。符號含義及具體使用參數見表1。

表1 半掛車的動力學簡化模型參數

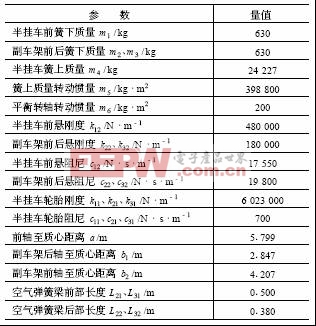
　　計算中模型的懸架系統的剛度和阻尼系數與輪胎剛度和阻尼系數均取左右兩側之和。

　　二、數學模型

　　（一）微分方程

　　根據給出的動力學模型，利用拉格朗日方程建立數學模型，其通式為

　　
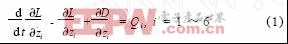
式中L為拉格朗日函數，L=T-V，其中T為系統動能，V為系統勢能；D為系統的耗散能；Q為系統的廣義力。

　　具體各項的表達式如下：

　　副車架前懸架后支撐位移z22的計算要考慮懸架前支撐位移z21的影響和前懸架質量塊m2位移z2的綜合影響，根據幾何關系有

　　同理可以得到副車架后懸架后支撐位移Z32。

　　將式（2）～式（4）代入式（1）得到

　　式中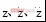 分別為位移、速度和加速度列向量。
M、C、K分別為質量、阻尼和剛度矩陣。Q為路面激勵力的列向量，文中假設輪胎阻尼為0，則 。