基于CORDIC算法2FSK調(diào)制器的FPGA設計
加入技術交流群
為了避免復雜的乘法運算，用一系列微旋轉來處理，第i次旋轉可表示為：
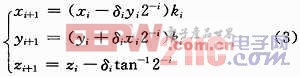
式中：θi表示第i次旋轉的角度，并且滿足tanθi=2-i；zi表示第i次旋轉后與目標角度的差；δi表示向量的旋轉方向，由zi的符號位來決定，即δi=sign zi。
為每一級的校正因子，也就是每一級旋轉時向量模長發(fā)生的變化，對于字長一定的運算，總的校正因子是一個常數(shù)。若總的旋轉次數(shù)為n，則總校正因子用k表示為：
由式(7)可知：xn，yn分別為輸入角θ的余弦和正弦值，故基于CORDIC算法可產(chǎn)生正弦載波信號，而且由式(5)可以看出所有運算簡化成加減法和移位操作，因此很容易用硬件實現(xiàn)。本文引用地址：http://www.104case.com/article/191186.htm
1．2 CORDIC流水線結構
CORDIC算法的實現(xiàn)方式有2種：簡單狀態(tài)機法和高速全流水線處理器法。如果計算時間的要求不嚴格，可以采用狀態(tài)機結構。這一結構中最復雜的就是兩個桶狀移位器，而桶狀移位器的面積大約和它所包含的傳輸門的數(shù)目成正比。盡管可以通過改進CORDIC算法來減小CORDIC處理器的總面積，但桶狀移位器所占的面積并不能減小。另外，這種結構由于只在時間上復用資源，因此，數(shù)據(jù)吞吐率不高。
評論