線性調(diào)頻信號(hào)基于FPGA IP核的脈沖壓縮設(shè)計(jì)
2.2.1 FFT運(yùn)算
對(duì)于長(zhǎng)度為N的時(shí)域序列X(n)的離散傅里葉變換為X(k):
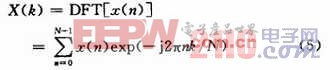
FFT算法主要是利用旋轉(zhuǎn)因子exp(-j2πnk/N)的周期性和對(duì)稱性的特點(diǎn)進(jìn)行改進(jìn)的算法,可以有效地減小運(yùn)算量。Xilinx公司的FFT核利用Cooley-Tukey算法實(shí)現(xiàn)FFT/IFFT運(yùn)算,最高支持216點(diǎn)長(zhǎng)度的運(yùn)算,可以實(shí)現(xiàn)流水線型、基4、基2三種結(jié)構(gòu),蝶形運(yùn)算后可選擇對(duì)數(shù)據(jù)順序輸出還是倒序輸出,對(duì)IP核進(jìn)行不同的配置,可以實(shí)現(xiàn)資源和運(yùn)算速度的最優(yōu)化。在此選用基4蝶形運(yùn)算,對(duì)于1 024點(diǎn)數(shù)據(jù),需要5級(jí)蝶形運(yùn)算。
Xilinx公司的FFT核的參數(shù)通過(guò)GUI界面(見(jiàn)圖5)進(jìn)行設(shè)置,可設(shè)置的參數(shù)包括FFT點(diǎn)數(shù),運(yùn)算實(shí)施方法,輸入數(shù)據(jù)位數(shù)等,設(shè)置完畢后點(diǎn)擊Generate可即時(shí)生成代碼。本文引用地址:http://www.104case.com/article/191135.htm

硬件描述語(yǔ)言采用VHDL,使用時(shí)程序中要對(duì)器件初始化并進(jìn)行定義,F(xiàn)FT核的器件定義語(yǔ)句見(jiàn)圖6。

2.2.2 匹配濾波系數(shù)產(chǎn)生
根據(jù)匹配濾波理論,對(duì)于一個(gè)確定的輸入信號(hào),匹配濾波系數(shù)就是這個(gè)輸入信號(hào)的頻譜的復(fù)共軛,系數(shù)可以通過(guò)Matlab預(yù)先計(jì)算出來(lái)并以二進(jìn)制的文件格式進(jìn)行存儲(chǔ)。此處計(jì)算時(shí)可以進(jìn)行加權(quán)處理,在系數(shù)中乘以窗函數(shù)即可。
通過(guò)Xilinx公司的單口Block Memory核,可以把Matlab產(chǎn)生的存儲(chǔ)文件加載進(jìn)去。當(dāng)程序運(yùn)行時(shí),根據(jù)使能控制信號(hào),把匹配濾波系數(shù)數(shù)據(jù)(1 024點(diǎn))依次讀取出來(lái),送入乘法器進(jìn)行后續(xù)運(yùn)算。BlockMemory核的參數(shù)設(shè)置通過(guò)GUI界面進(jìn)行,可即使生成代碼。
2.2.3 乘法運(yùn)算
乘法運(yùn)算部分完成FFT后數(shù)據(jù)與匹配濾波系數(shù)數(shù)據(jù)的復(fù)數(shù)乘法運(yùn)算。根據(jù)復(fù)數(shù)的乘法規(guī)則。
(A+aj)(B+bj)=(AB-ab)+(Ab+aB)j
兩個(gè)復(fù)數(shù)的乘法運(yùn)算實(shí)際上包括了4個(gè)實(shí)數(shù)的乘法運(yùn)算,因此,此部分的設(shè)計(jì)用到了4個(gè)乘法器核。Xilinx公司的乘法器核支持補(bǔ)碼運(yùn)算,可輸入A,B兩路數(shù)據(jù),每路的輸入數(shù)據(jù)長(zhǎng)度可達(dá)64 b。乘法器核的參數(shù)設(shè)置也是通過(guò)GUI界面進(jìn)行,可即使生成代碼。















評(píng)論