基于CPLD的溫度自動控制系統的研制
溫度自動控制系統的軟件算法通常是根據對象的純滯后時間τ與對象的慣性時間常數Tm之比來確定,一般來說,當τ/Tm0.5時,可采用PID算法控制,當τ/Tm>0.5時,可采用達林算法控制。在本系統中,針對不同的被控對象,可加載不同的軟件算法,因此大大提高了本控制系統的靈活性。由于在工業控制過程中,大量的被控對象具有非線性、純滯后性,采用PID控制很難獲得良好的控制性能,因此本文重點討論達林算法,用它來控制非線性、純滯后對象具有良好的效果(被控對象一般為帶有滯后的一階慣性環節)。
2.1 dahlin算法的數學模型
被控對象為帶有滯后的一階慣性環節,其傳遞函數為
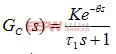
,θ=NT (2-1)
式中:τ1 -----對象的時間參數
θ -----對象的純延遲時間,為了簡化,設其為采樣周期的整數倍,即N為正整數。
K -----對象放大系數
達林算法的設計目標是使整個閉環系統所期望的傳遞函數Φ(s),相當于一個延時環節和一個慣性環節相串聯,即
Φ(s)=
,θ=NT (2-2)
如圖6所示,根據控制理論易得到帶有一階慣性對象的達林算法的基本形式:
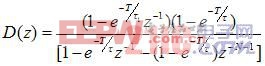
×
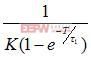
(2-3)
式中:K -----對象放大系數
T ------ 為采樣周期;
τ1 ------為被控對象時間參數;
τ ------為閉環系統的時間參數。
根據D(Z)=U(Z)/E(Z)得出差分方程:
U(K)=b1U(K-1)+b2U(K-N-1)+a0E(K)-a1E(K-1) (2-4)
其中
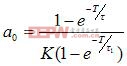
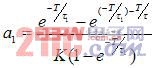
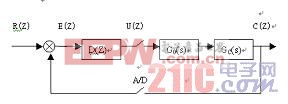
圖6 控制系統方框圖








評論