基于MATLAB的線性二次型最優控制

對比仿真結果可以看出，當小車擺桿角度權重選定為合適的值，隨著小車位置權重的增加，小車位移系統階躍響應超調減小，上升時間和調整時間也加快。與此同時，也引進了一些振蕩。

5.2 加權矩陣R的研究

從降低控制系統能量要求優先角度出發，讓Q不變，R減小。這時由Riccati方程求得的系統反饋增益陣K增大。例如R=0.01時，相應的K=[-175.4699,-46.1765,-10.0000,-20.8841]。

改變加權陣Q后的響應結果如圖6，控制力輸出曲線如圖7

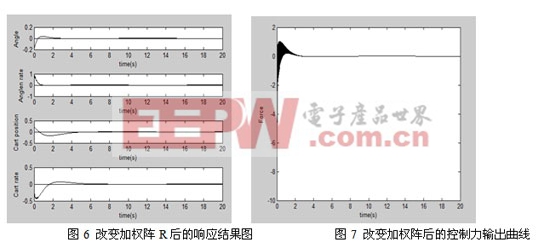
對比仿真結果可以看出，調整時間與超調量減小，上升時間與穩態誤差減小。但是系統穩定性很差，時控過程噪聲很大。

6 結束語

本文針對倒立擺系統進行數學建模，采用最優控制中的LQR控制方法，對系統進行局部的線性化，通過仿真實驗得到該方法作用于倒立擺系統是可行且有效的，同時分析了加權矩陣Q和R對系統性能指標的影響。

參考文獻：

[1] 劉金亨，陳今潤，呂郁青，等. 基于LQR的一階直線雙倒立擺最優控制系統研究[J].自動化技術與應用，2009,28(5)：11-13.

[2] 槐創鋒，方躍法. 5連桿雙足機器人建模和控制系統仿真[J].系統仿真學報，2008，20(20)：82-86.

[3] 李德毅，杜鶿. 不確定性人工智能[M].北京：國防工業出版社，2005.

[4] 姜春瑞. 基于云模型理論的一階直線倒立擺控制技術研究[D]. 哈爾濱工業大學，2005.

[5] 劉豹. 現代控制理論[M]. 北京：機械工業出版社，2007.

[6] 劉金琨. 先進PID控制及其MATLAB仿真[M]. 北京：電子工業出版社，2003.1.