基于ANFIS 的有色噪聲抵消技術

其中：s(k)為有用信號；c(k)為可測噪聲，經過非線性變換H(z)后為有色噪聲z(k) ，測量信號d(k) =s(k)+ z(k) 為被噪聲污染的信號，s(k)與 z(k) 是不相關的。噪聲抵消就是從被噪聲污染的信號中估計s(k)，顯然，這只要估計出z（k）即可。而z(k)是c(k)的延遲和變形，它是不可測的，即z(k)=f(c(k),c(k-1,c(k-2),…) ，其中，函數f 是未知的、非線性的，而且其頻率范圍往往與d(k)的頻率范圍重疊，所以，頻率濾波技術無法實現。現在利用ANFIS 網絡可以任意逼近非線性函數的能力，使ANFIS 網絡逼近有色噪聲z(k)，從而估計出信號y(k) 。

用ANFIS 網絡逼近有色噪聲時，網絡的輸入為噪聲c(k)和c(k-1) ，并且每個變量采用鐘形隸屬函數，輸出樣本本應該為有色噪聲，但是實際不能直接得到它，這里可以用測量信號d(k)=s(k)+f(c(k),c(k-1),…)來代替。ANFIS 的輸出即可作為z（k）的估計值.()，而ANFIS 的訓練應使下面的誤差最小

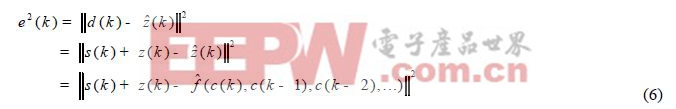
其中f.就是由ANFIS 產生的非線性函數的逼近。將上式展開，得

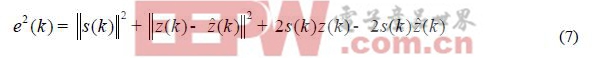
信號s(k)。

3 仿真研究

設有用信號為

利用MATLAB 仿真，ANFIS 的信息如下：

Number of nodes: 21
Number of linear parameters: 12
Number of nonlinear parameters: 12
Total number of parameters: 24
Number of training data pairs: 601
Number of checking data pairs: 0
Number of fuzzy rules: 4

結果如圖3 所示。

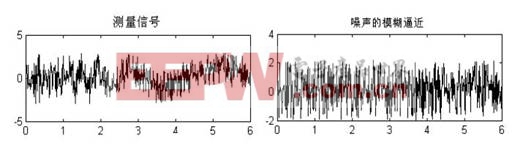
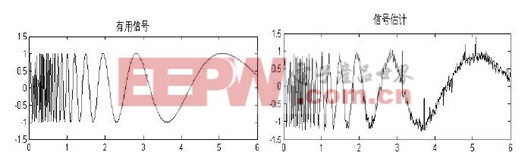
圖3 仿真結果

4 結論

自適應噪聲抵消技術，可在未知外界干擾源特征、傳遞途徑不斷變化，以及背景噪聲和被測對象相似的情況下，能夠有效地消除外界聲源的干擾獲得高信噪比的對象信號，這一技術可為機械元件的噪聲、振動等動態信號在測試環境不太理想的工作現場做測試分析和故障診斷時，提供可靠的方法和依據，具有一定的理論意義和應用價值。

本文作者創新點：對用ANFIS 網絡逼近有色噪聲進行了誤差分析，進而從測量信號中消除有色噪聲得到有用信號。