基于數字電路中卡諾圖的應用研究

根據或運算的特點，求或運算時，只要將Y1、Y2卡諾圖中出現的所有l都畫入包圍圈，然后根據卡諾圖寫出表達式。
2)求兩邏輯函數Fl和F2的與運算Fl?F2
根據與運算的特點，求與運算時，只要將F1、F2卡諾圖中重復出現的l畫入包圍圈，然后根據卡諾圖寫出表達式。
3)求兩邏輯函數Fl和F2的異或運算Fl+F2
根據異或運算的特點，求異或運算時，只要將Fl、F2卡諾圖中不重復出現的l畫入包圍，然后根據卡諾圖寫出表達式。
例：已知兩邏輯函數F1(A，B，C)=∑m(0，1，3)，F2(A，B，C)=∑m(0，4，5，7)，試用卡諾圖分別求出F1+F2；Fl?F2和Fl+F2。
解：
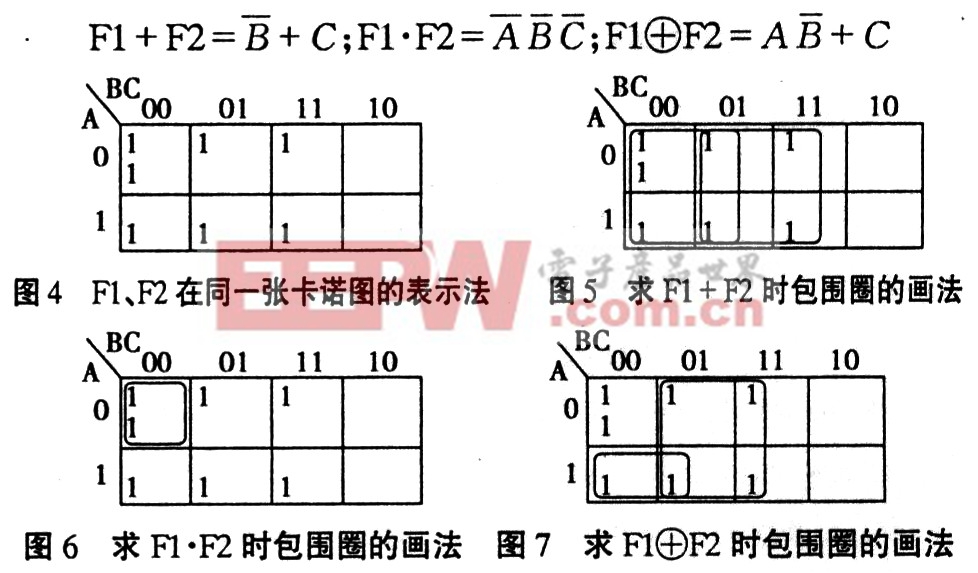
1)將邏輯函數Fl、F2在同一張卡諾圖中表示出來，將函數出現的1填在卡諾圖小方格的左上角，將函數F2出現的l填在卡諾圖小方格的左下角，如圖4；
2)求Fl+F2時，將Fl、F2卡諾圖中出現的所有l都畫入包圍圈，如圖5；
3)求F1?F2時，將F1、F2卡諾圖中重復出現的1畫入包圍圈，如圖6；
4)求F1+F2時，將F1、F2卡諾圖中不重復出現的1畫入包圍圈，如圖7；
5)根據圖5、6、7寫出函數表達式：

1．4 使用降維卡諾圖化簡多變量函數
在卡諾圖中，通常我們用“0”、“1”以及無關項“d”(或用“×”表示)作為卡諾圖中的單元值，函數的變量都作為卡諾圖的變量，一般來說，卡諾圖的維數也就是函數的變量數．如果將某些變量也作為圖中的單元值，則所得到的卡諾圖維數將減少，這樣的卡諾圖叫做降維卡諾圖。在用中規模集成電路，特別是用數據選擇器來實現函數時，使用降維卡諾圖化簡多變量函數是非常有用的。降維卡諾圖化簡原理在此不再贅述。
例如邏輯函數F(A，B，C，D)=∑m(0，3，5，6，9，10，12，
15)如果選用8選1數據選擇器74LSl5l實現組合邏輯函數，由于8選l數據選擇器的地址變量為3個，將邏輯函數降維為三維卡諾圖后與8選1數據選擇器含Di的卡諾圖對照比較(見圖8)，很容易獲得數據選擇器輸入信號與邏輯函數變量的關系：令A2=A，A1=B，A0=C，則Do=D3=D5=D6=D，Dl=D2=D4=D7=D，畫出邏輯圖，如圖9所示。

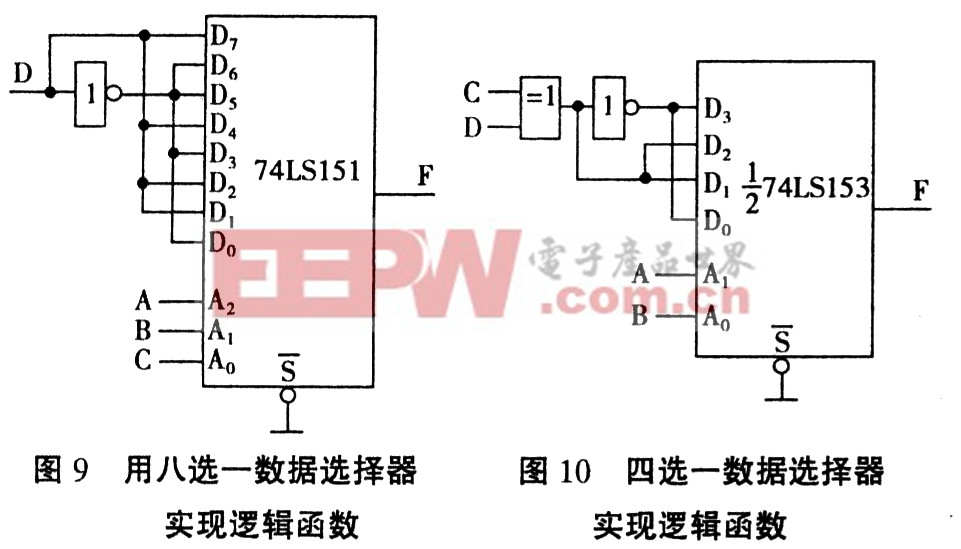
如果選用4選一數據選擇器實現邏輯函數，還可以將三維卡諾圖繼續降維成二維卡諾圖后與4選l數據選擇器含Di的卡諾圖對照比較(見圖11)，獲得數據選擇器輸入信號與邏輯函數變量的關系：A1=A，A0=B，D0=D3=CD+CD=C+D，Dl=D2=CD+CD=C+D
用4選一數據選擇器實現邏輯函數見圖10。

2 結束語
從以上幾例論述可知，卡諾圖的用途不只限于邏輯函數化簡的功能，可廣泛用于記憶或設計有關碼制，競爭冒險中的判斷，數據選擇器實現組合邏輯函數和邏輯函數的邏輯運算等，深入理解卡諾圖的內涵，巧妙地應用它，能得到意想不到的效果，為數字邏輯電路的分析和綜合帶來很大的方便。