一種提高DSP的ADC精度的方法

0 引言
TI公司的C2000系列DSP以其出色的性能、豐富的片上外設在工業自動化、電機控制、工業生產領域得到廣泛應用。TMS320F2812是C2000系列中性能出色的一個，F2812片上集成了12位16通道的數／模轉化器，理論上精度可以達到0．1％以上。但實際上由于增益誤差(5％)和偏移誤差(2％)的存在，使得精度只能在5％左右，所以必須對ADC進行校正。
傳統的對于ADC的校正方法是在兩路通道輸入已知標準電壓，根據兩點確定一條直線的原理，確定出AD轉換的曲線，并以此校正轉化值。但由于在校正過程中存在偶然因素的影響，使得這種校正方法精度只能達到3％左右。對此，提出了利用最小二乘法和線性回歸的思想進行校正的方法，通過對多個測量點的分析計算，找出最佳的擬合曲線，使得總體的均方誤差最小。
最小二乘法是高斯于1809年提出的，在多學科領域中獲得廣泛應用的數據處理方法。用最小二乘法估測未知參數，可以有效消除測量中粗大誤差和系統誤差的影響。回歸分析是英國統計學家高爾頓在1889年首先提出的。一元線性回歸是利用數理統計中的回歸分析，來確定兩種或兩種以上變數間相互依賴的定量關系的一種統計分析方法之一，運用十分廣泛。一般來說，線性回歸都可以通過最小二乘法求出其方程，可以計算出對于y=bx+a的直線。

1 校正原理與實現方案
DSP的ADC模塊的輸入、輸出是線性關系，理想情況下，輸入輸出方程應該是y=x。但實際上，ADC模塊是存在增益誤差和偏移誤差的，其中增益誤差是實際曲線斜率和理想曲線斜率之間的偏差，偏移誤差是0 V輸入時實際輸出值與理想輸出值(0 V)之間的偏差。F2812的ADC模擬輸入電壓為0～3 V，輸出為0～4 095，模擬輸入與數字輸出之間的對應關系為：數字輸出值=4 095×(模擬輸入值-參考電壓值)／3．OADC模塊輸入／輸出特性曲線如圖1所示。

F2812的ADC共有輸入通道16個，由于通道之間的誤差會在±0．2％以內，所以可以任選其中的6路通道作為校正輸入端，并分別輸入6個不相等的標準直流參考電壓。通過在程序中定義結構體變量讀取轉化后的值，得到6組輸入／輸出平面上的坐標點。然后利用最小二乘和一元線性回歸思想處理數據，求出的擬合最佳曲線，使得各個坐標點到該最佳曲線的距離的平方和(殘差平方和)最小。

2 最小二乘法和一元線性回歸
2．1 最小二乘原理
對于線性模型，如果有t個不可測量的未知量，理論上，可對與該t個未知量有函數關系的直接測量量進行t次測量，即可得到函數關系。但由于測量數據不可避免地包含著測量誤差，所得到的結果也必定含有一定的誤差。為了提高所得結果的精度，可以把測量次數增加到n(n>t)，以利用抵償性減小隨機誤差的影響。
高斯認為，根據觀測數據求取未知參數時，未知參數最合適數值應是這樣的數值，即選出使得模型輸出與觀測數據盡可能接近的參數估計，接近程度用模型輸出和數據之差的平方和來度量。這就是最小二乘的基本思想。最小二乘法原理指出，最精確的值應在使殘余誤差平方和最小的條件下求得。
2．2 一元線性回歸原理
一元線性回歸是處理2個變量之間的關系，即兩個變量x和y之間若存在線性關系，則通過試驗，分析所得數據，找出兩者之間函數曲線。也就是工程上常遇到的直線擬合問題。

3 實驗方案與結果分析
3．1 實驗方案
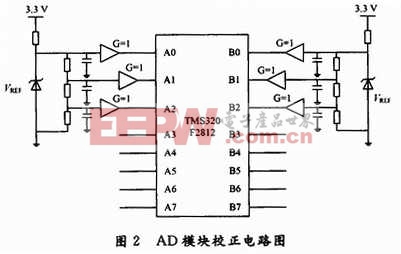
實驗利用F2812開發板和DSP調試軟件CCS2．0完成。用穩定信號源產生6個標準電壓，分別為0．2 V，0．5 V，1．0 V，1．5 V，2．0 V，2．5 V，輸入通道選為A0，A1，A2，B0，B1，B2。ADCL0引腳接電路板的模擬地，與模擬輸入引腳相連的信號線應該避開數字信號線，以減少數字信號對模擬信號的干擾。輸入電路如圖2所示。