利用抖動(dòng)改進(jìn)通信系統(tǒng)應(yīng)用中ADC的SFDR
了解更多關(guān)于抖動(dòng)的信息,即改善表現(xiàn)出差分非線性(DNL)誤差的模數(shù)轉(zhuǎn)換器(ADC)的無雜散動(dòng)態(tài)范圍(SFDR)。
本文引用地址:http://www.104case.com/article/202501/465964.htm在上一篇文章中,我們討論了如何通過打破量化誤差和輸入信號(hào)之間的統(tǒng)計(jì)相關(guān)性來使用抖動(dòng)來提高理想量化器的性能。理想情況下,我們的意思是ADC傳遞函數(shù)具有均勻的步長。換句話說,理想的ADC具有零DNL誤差。抖動(dòng)的這種應(yīng)用在需要高SFDR的無線電接收機(jī)中尤為重要。
在本文中,我們將討論抖動(dòng)的另一個(gè)重要應(yīng)用,即改善現(xiàn)實(shí)世界中出現(xiàn)DNL誤差的a/D轉(zhuǎn)換器(如AD6645)的SFDR。抖動(dòng)的這種應(yīng)用在當(dāng)今需要高SFDR的無線電接收機(jī)中尤為重要。
ADC靜態(tài)和動(dòng)態(tài)線性度
在開始之前,讓我們先快速回顧一下提高ADC線性度的主要局限性。盡管ADC使用不同的架構(gòu)和電路實(shí)現(xiàn),但它們有兩個(gè)主要的非線性源:采樣保持(S/H)電路和ADC的編碼器部分。S/H非線性的一部分源于這樣一個(gè)事實(shí),即它的轉(zhuǎn)換速率有限,當(dāng)輸入是具有大振幅的高頻信號(hào)時(shí),可能無法足夠快地跟隨輸入。缺乏表現(xiàn)出足夠轉(zhuǎn)換速率的S/H是許多ADC無法提供高于幾兆赫信號(hào)帶寬的高SFDR的關(guān)鍵原因。這也解釋了為什么S/H的非線性是頻率相關(guān)的。S/H在確定ADC的動(dòng)態(tài)(或AC)線性度方面起著關(guān)鍵作用。
另一個(gè)非線性源是ADC編碼器部分。對(duì)于給定的ADC相位,編碼器部分主要處理DC信號(hào),因?yàn)樗挥赟/H之后。因此,編碼器非線性對(duì)系統(tǒng)的靜態(tài)(或DC)非線性有貢獻(xiàn)。這種非線性成分在理想情況下不會(huì)隨頻率變化。靜態(tài)非線性的特征是ADC傳遞函數(shù)中的DNL和INL(積分非線性)誤差。“靜態(tài)非線性”一詞可能用詞不當(dāng),因?yàn)檫@種非線性分量不僅影響直流信號(hào),在處理交流信號(hào)時(shí)還會(huì)降低線性度。
注意哪種非線性類型占主導(dǎo)地位!
本文要記住的另一件重要事情是,對(duì)于許多ADC,S/H是非線性的主要來源。在這種情況下,隨著輸入接近奈奎斯特頻率,諧波失真性能迅速下降。如果S/H是限制因素,那么外部無法顯著提高ADC的線性度。然而,一些ADC是專門設(shè)計(jì)的,具有寬帶、高度線性的前端。這使得編碼器部分成為非線性的主要來源。使用這種ADC,我們可以使用抖動(dòng)技術(shù)來提高ADC的SFDR。在研究抖動(dòng)的這種應(yīng)用之前,讓我們仔細(xì)看看ADC靜態(tài)傳遞函數(shù)引入的非線性誤差。
傳遞函數(shù)非線性——確定性誤差
為了更好地理解靜態(tài)非線性,我們將以圖1所示的傳遞函數(shù)引入的非線性誤差為例進(jìn)行研究。
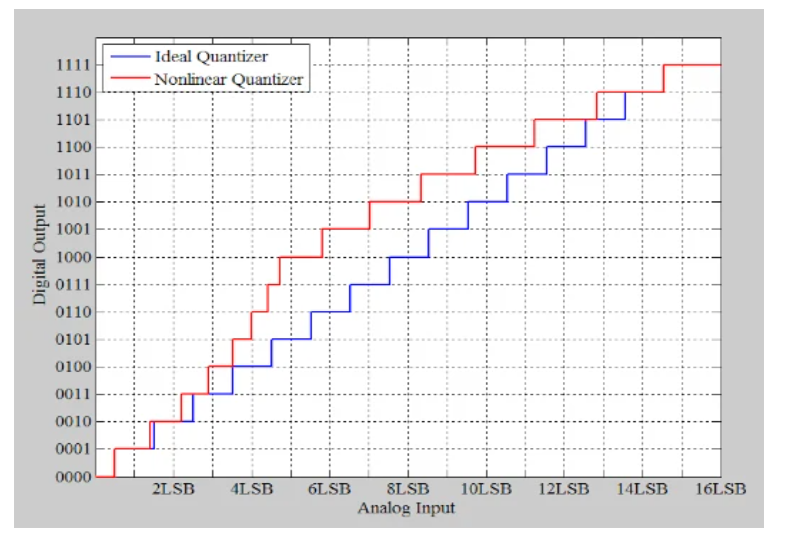
圖1 引入非線性誤差的傳遞函數(shù)示例
上圖中的紅色曲線顯示了非線性4位ADC,而藍(lán)色曲線顯示了理想的4位響應(yīng)。如果我們使用上述特征曲線對(duì)以4 MHz采樣的1.11 kHz正弦曲線進(jìn)行數(shù)字化,我們將在圖2中獲得以下波形。
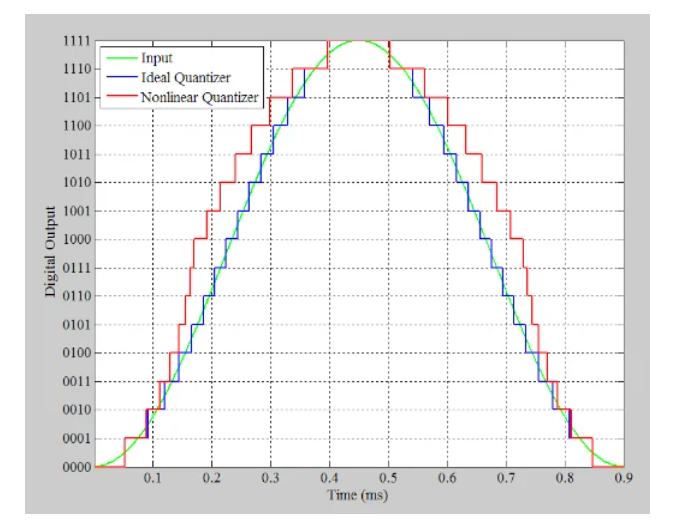
圖2 以4 MHz采樣的數(shù)字化1.11 kHz正弦波的波形
在圖2中,綠色曲線顯示了輸入,而藍(lán)色和紅色曲線分別是理想和非線性傳遞函數(shù)的輸出。通過從紅色曲線中減去藍(lán)色曲線,我們可以確定非理想響應(yīng)引入的非線性誤差。如圖3中的紅色曲線所示。
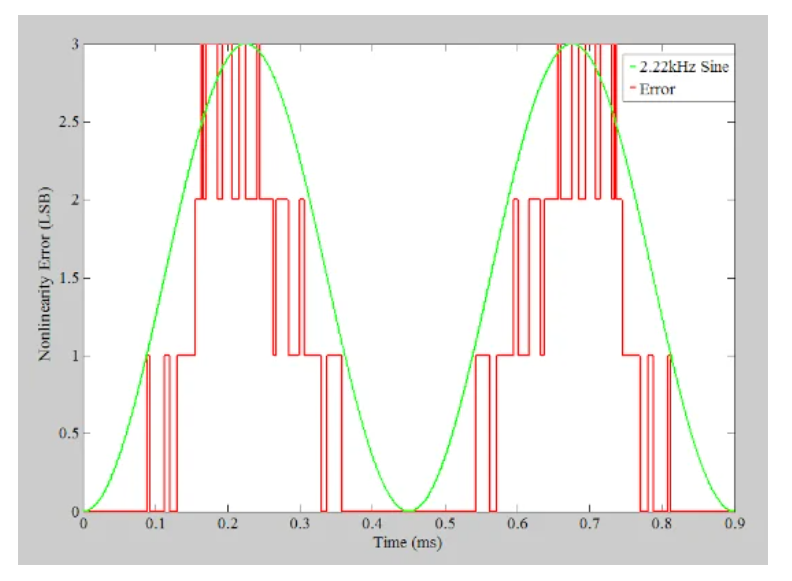
圖3顯示非理想響應(yīng)引入的非線性誤差的圖
傳遞函數(shù)非線性引入的誤差是確定性誤差。這意味著,對(duì)于給定的輸入電壓,誤差總是相同的。例如,參考圖1,我們觀察到6個(gè)LSB(最低有效位)的輸入總是導(dǎo)致比理想值高3個(gè)LSB的輸出。這種確定性行為在輸入和錯(cuò)誤之間建立了相關(guān)性。如果輸入處于特定頻率,我們預(yù)計(jì)誤差在與輸入相關(guān)的某些特定頻率處具有很強(qiáng)的頻率分量。
圖3可以幫助您更好地理解這種情況。在這種情況下,誤差波形不是精確的周期性的;然而,錯(cuò)誤的整體形狀似乎以有規(guī)律的方式重復(fù)出現(xiàn)。也就是說,在輸入信號(hào)的一個(gè)周期內(nèi)有兩次重復(fù)。這表明誤差在輸入的二次諧波處具有很強(qiáng)的分量。為了更好地可視化這一點(diǎn),該圖還繪制了2.22 kHz(二次諧波)的正弦波。如您所見,正弦波近似于誤差波形整體形狀的趨勢。
對(duì)非線性響應(yīng)輸出進(jìn)行快速傅里葉變換(FFT),我們得到了下圖4中的頻譜,其中僅顯示了DC到50kHz的范圍。
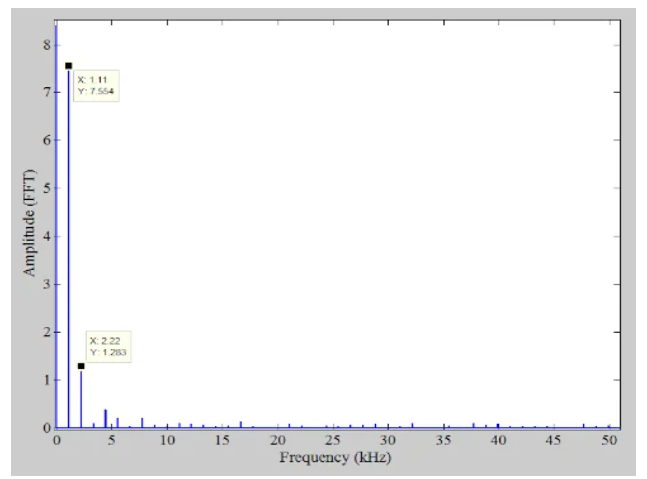
圖4 顯示從直流到50 kHz范圍的非線性響應(yīng)輸出的圖
FFT結(jié)果證實(shí),二次諧波是非線性響應(yīng)的主頻分量。值得一提的是,主要諧波分量的頻率取決于ADC的INL形狀。對(duì)于圖1所示的非線性,有時(shí)被稱為弓形INL,二次諧波是主要的。對(duì)于S形INL,三次諧波是誤差的主要頻率分量。有關(guān)INL形狀對(duì)D/a轉(zhuǎn)換器(DAC或數(shù)模轉(zhuǎn)換器)頻譜影響的討論,請(qǐng)參閱本文。
打破ADC誤差與輸入之間的相關(guān)性
如果我們?cè)谳斎攵颂砑右粋€(gè)相對(duì)較大的隨機(jī)信號(hào),使ADC的整體輸入在ADC傳遞函數(shù)的不同步驟之間以不可預(yù)測的方式變化,我們可以在一定程度上減少確定性失真。這一概念如圖5所示。
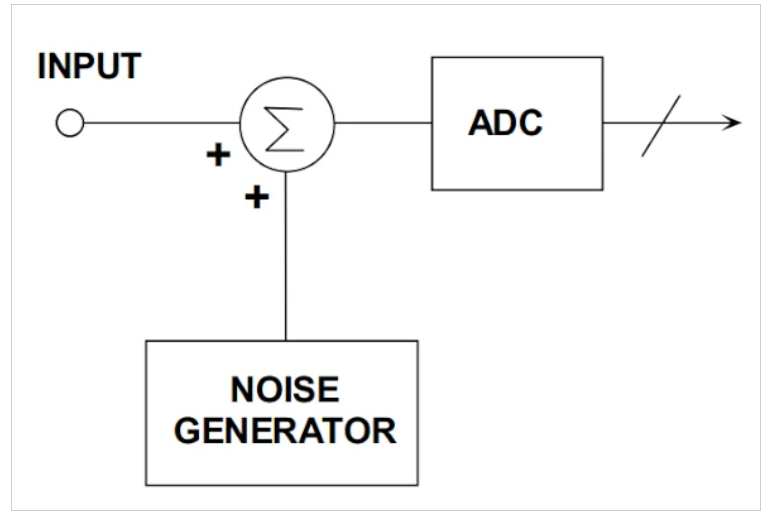
圖5 顯示ADC傳遞函數(shù)步驟期間ADC輸入變化的基本圖。圖片由ADI公司提供
添加隨機(jī)信號(hào)(或抖動(dòng)信號(hào))后,給定的輸入并不總是轉(zhuǎn)換為相同的輸出電平。因此,即使輸入恒定,誤差也會(huì)隨著時(shí)間而變化。例如,考慮將6個(gè)LSB的輸入應(yīng)用于圖1中的傳遞函數(shù)。如果沒有抖動(dòng),誤差總是3個(gè)LSB。現(xiàn)在考慮一下這個(gè)懸而未決的案子。假設(shè)抖動(dòng)信號(hào)偶爾等于2個(gè)LSB。在2個(gè)LSB處,非線性誤差變?yōu)榱恪S捎谡`差在0到3個(gè)LSB之間變化,因此與未受影響的情況相比,誤差平均值減小了。這個(gè)簡單的例子展示了抖動(dòng)如何消除輸入和非線性誤差之間的相關(guān)性,從而減少確定性失真。抖動(dòng)通過使轉(zhuǎn)換器的DNL誤差非定域或隨機(jī)化來實(shí)現(xiàn)這一點(diǎn)。通過消除與輸入的誤差相關(guān)性,諧波分量被傳播到噪聲基底中,SFDR得到改善。
通信系統(tǒng)抖動(dòng)技術(shù)
抖動(dòng)技術(shù)在通信系統(tǒng)中特別有用。對(duì)于許多通信應(yīng)用,輸入可以是遠(yuǎn)低于ADC滿量程的小信號(hào)。這個(gè)小信號(hào)執(zhí)行相對(duì)較少的ADC代碼。如果這些代碼表現(xiàn)出較大的DNL誤差,則輸出將包含明顯的諧波失真。
請(qǐng)注意,對(duì)于滿標(biāo)度(或大)信號(hào),DNL誤差在某種程度上是固有的平均值。原因是大信號(hào)會(huì)執(zhí)行ADC的所有代碼。因此,當(dāng)信號(hào)幅度降低到比滿量程值低20dB時(shí),表現(xiàn)出88dBFS的滿量程SFDR的ADC可能只提供80dBFS的SFDR。在這種情況下,抖動(dòng)技術(shù)可能有助于我們?cè)诘托盘?hào)電平下保持ADC的SFDR性能。應(yīng)當(dāng)注意,由于輸入電平較小,我們可以在不過度驅(qū)動(dòng)ADC的情況下將抖動(dòng)信號(hào)添加到輸入端。
ADC噪聲——我們不是在丟失信息嗎?
你可能會(huì)問:我們不是因?yàn)樵谳斎胄盘?hào)中添加了相對(duì)較大的噪聲而丟失了信息嗎?答案是信息似乎在時(shí)域中丟失了。然而,正確選擇噪聲信號(hào)以及信號(hào)處理技術(shù),使我們能夠重建原始信息。一種解決方案是減法抖動(dòng)。在這種情況下,圖5中的基本圖被修改為下圖(圖6)。
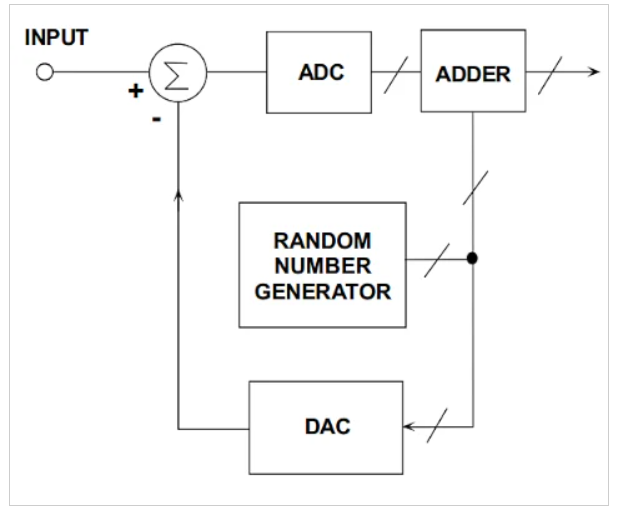
圖6 減法抖動(dòng)圖。圖片由ADI公司提供
在減法中,引入輸入端的噪聲以相反的極性添加到輸出端,從而消除系統(tǒng)輸出端的凈抖動(dòng)噪聲。另一種用于通信系統(tǒng)的有趣技術(shù)是使用頻率內(nèi)容在所需信號(hào)帶寬之外的窄帶噪聲。幾百kHz的小帶寬通常足以用于抖動(dòng)信號(hào)。帶外噪聲的兩個(gè)可能位置接近直流或略低于奈奎斯特頻率(fs/2,其中fs是采樣頻率)。這兩個(gè)頻率區(qū)中的一個(gè)不用于大多數(shù)可用于抖動(dòng)目的的通信系統(tǒng)。在這種情況下,抖動(dòng)可以很容易地在輸出端被過濾掉。
使用我們的假想ADC
讓我們使用圖1中的傳遞函數(shù)來檢查這種技術(shù)。為此,我們將振幅為2 LSB、直流值為7.5 LSB的1.11 kHz正弦曲線應(yīng)用于該ADC。這樣的輸入練習(xí)ADC的中頻碼。從略高于0 Hz到30 kHz范圍的輸出頻譜如圖7所示。
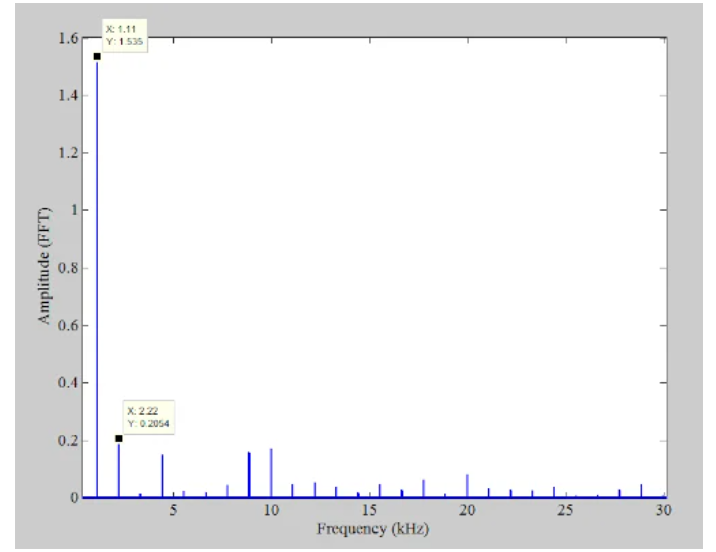
圖7 1.11 kHz正弦曲線的另一個(gè)示例圖,其頻譜范圍從略高于0 Hz到30 kHz
對(duì)于這種特殊的輸入,有幾個(gè)不同的諧波分量,但主要的仍然是二次諧波。將這些值轉(zhuǎn)換為分貝,我們發(fā)現(xiàn)SFDR為17.47 dBc。為了產(chǎn)生抖動(dòng)信號(hào),我們可以使用Matlab的“randn”函數(shù)產(chǎn)生具有2個(gè)LSB RMS(均方根)的寬帶高斯噪聲。應(yīng)用以1.94 MHz為中心的通帶為100 kHz的帶通濾波器,寬帶噪聲被轉(zhuǎn)換為略低于fs/2的窄帶抖動(dòng)。抖動(dòng)信號(hào)的頻譜如下圖8所示。
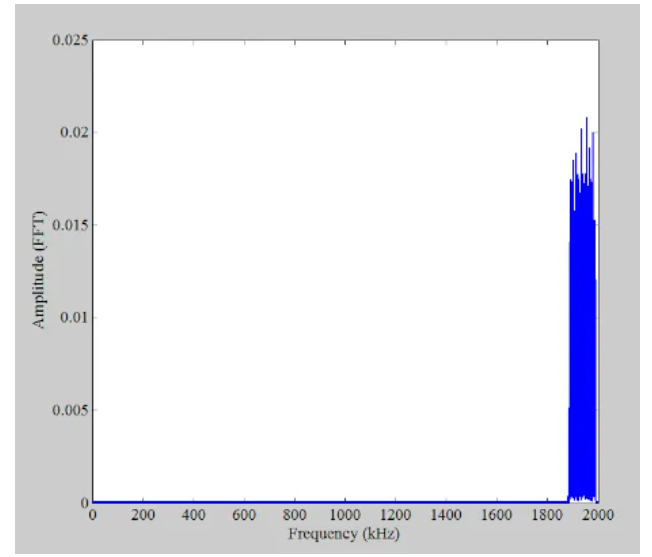
圖8 抖動(dòng)信號(hào)的示例頻譜
由于抖動(dòng)信號(hào)是原始噪聲的帶限版本,我們可以使用以下方程來確定抖動(dòng)信號(hào)的方差:
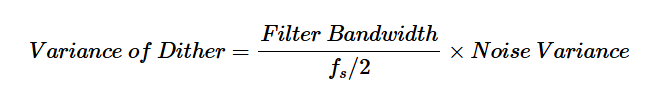
插入數(shù)字,我們得到:
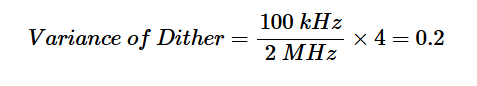
取該值的平方根,抖動(dòng)信號(hào)的均方根為0.45 LSB。抖動(dòng)的峰峰值可以估計(jì)為6.6 x 0.45=2.97 LSB(RMS高斯噪聲通過乘以6.6轉(zhuǎn)換為峰峰值)。請(qǐng)注意,抖動(dòng)的峰峰值足夠小,不會(huì)使ADC過載。應(yīng)用抖動(dòng)后,我們得到以下輸出光譜(圖9)。
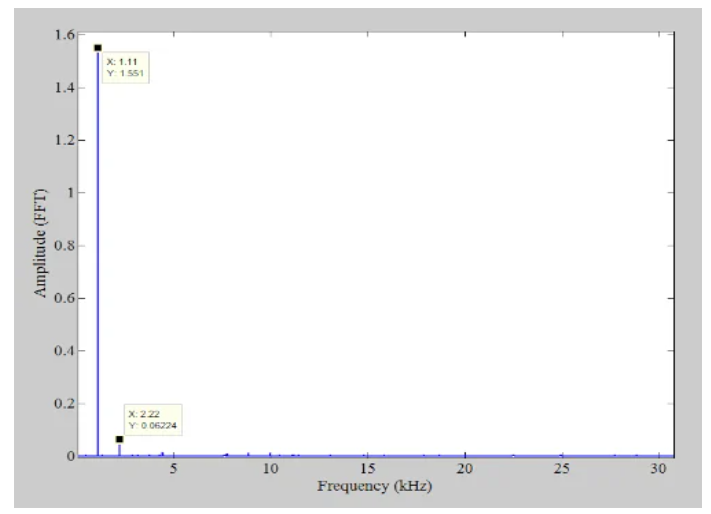
圖9 應(yīng)用抖動(dòng)RMS后的輸出光譜
可以看出,諧波得到了顯著抑制。將這些值轉(zhuǎn)換為分貝,我們得到的SFDR為27.9 dBc,與無阻尼的情況相比提高了10.43 dB。抖動(dòng)通過將信號(hào)雜散擴(kuò)展到噪聲基底來抑制諧波分量。
ADC3424模擬數(shù)字轉(zhuǎn)換器的測試結(jié)果
下圖10顯示了ADC3424在70 MHz輸入下的輸出頻譜。
ADC3424在70 MHz輸入下的輸出頻譜。
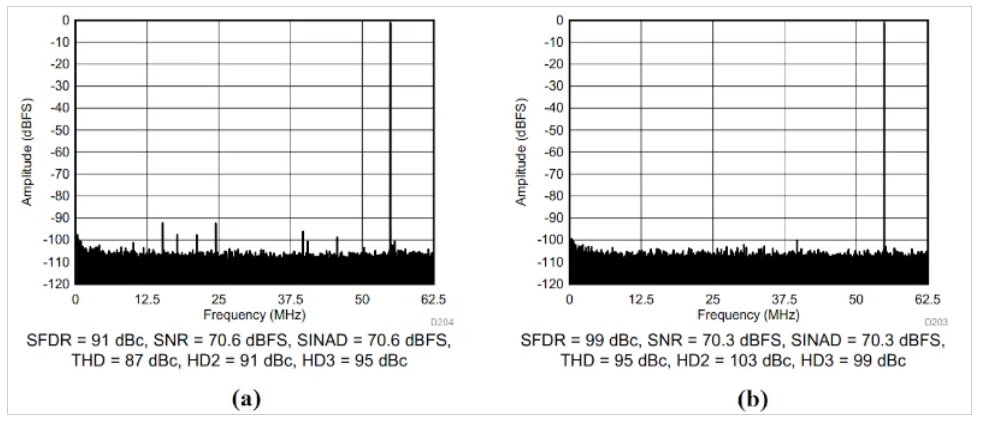
圖10 ADC3424在70 MHz輸入下的輸出頻譜。圖片由德州儀器提供
ADC3424提供抖動(dòng)功能作為內(nèi)部功能。關(guān)閉內(nèi)部抖動(dòng)后,SFDR為91 dBc。然而,隨著內(nèi)部抖動(dòng)的激活,雜散擴(kuò)展到本底噪聲中,SFDR增加到99 dBc。
抖動(dòng)技術(shù)限制
提供ADC SFDR顯著改善的適當(dāng)抖動(dòng)水平取決于該特定ADC的架構(gòu)和其他屬性。SFDR的改善還取決于輸入信號(hào)的幅度以及抖動(dòng)的幅度。還應(yīng)注意的是,超過一定水平的噪聲,SFDR可能不會(huì)顯著改善。例如,考慮ADI公司的AD6645。該設(shè)備采用多級(jí)架構(gòu)。使用這種類型的ADC架構(gòu),DNL誤差具有重復(fù)模式,當(dāng)輸入掃過ADC輸入范圍時(shí),DNL圖中會(huì)出現(xiàn)一些尖峰。下圖11顯示了AD6645在其輸入范圍的一小部分上的DNL圖。
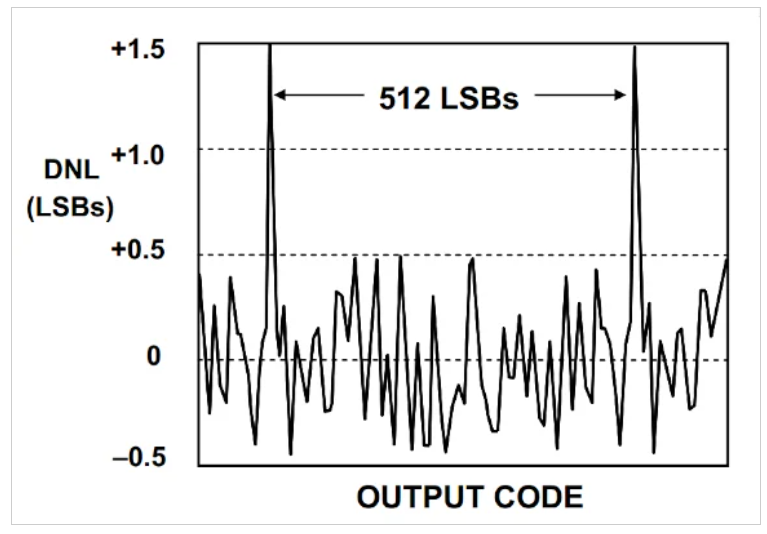
圖11 AD6645在其輸入范圍的一小部分上的DNL圖。圖片由ADI公司提供
在AD6645的情況下,尖峰每512個(gè)LSB出現(xiàn)一次。實(shí)驗(yàn)發(fā)現(xiàn),適用于這種特定ADC的抖動(dòng)水平為1024 LSB峰對(duì)峰或155 LSB RMS。應(yīng)用更大的抖動(dòng)并不能顯著提高AD6645的SFDR。對(duì)于該ADC,抖動(dòng)的峰峰值等于兩個(gè)DNL尖峰之間的碼距離的兩倍。然而,我們不能得出結(jié)論,這是所有多級(jí)ADC的一般規(guī)則。
要了解有關(guān)抖動(dòng)技術(shù)的更多信息,請(qǐng)參閱ADI公司的“用抖動(dòng)克服轉(zhuǎn)換器非線性”。









評(píng)論