模擬電路故障診斷的BP神經網絡方法研究
加入技術交流群
對于BP網絡，在閉區間內的任意一個連續函數都可以用單隱層的BP網絡逼近，即一個3層的BP網絡可以完成任意m維到n維的映射。由于有5個測試點，所以BP網絡的輸入層為5個神經元，以歸一化之后的數據作為BP網絡的輸入樣本，輸出層為4個神經元。隱層神經元數目的選擇是一個十分復雜的問題，往往需要根據經驗或者多次的實驗來判定，因而不存在一個確切的表達式來確定。它的數目與問題的要求、輸入／輸出單元的數目都有著直接關系。隱層單元數目太多會導致學習時間過長、誤差不一定最佳，也會導致容錯性差、不能識別以前沒有看到的樣本，因此一定存在一個最佳的隱單元數。此處參照美國科學家Hebb提出的以下經驗公式選取：
。其中：n為輸入單元數；m為輸出單元數；a為[1，10]之間的常數。按照上式，
，即h的取值為4～13。通過Matlab創建一個BP神經網絡，設定訓練次數為5 000，訓練目標net．trainParam．goal=0．01，改變隱層單元的數目，當隱層單元數不同時，達到目標所用的訓練次數，如表3所示。本文引用地址：http://www.104case.com/article/187386.htm
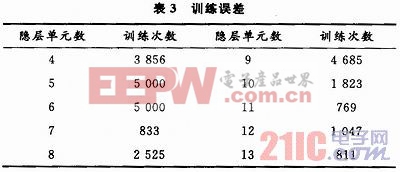
根據表3，當隱層單元數為11時，訓練次數最少，這樣神經網絡的結構就確定了，輸入層5個節點，隱層11個節點，輸出層4個節點，訓練最大次數設定為5 000，訓練誤差為0．01，先采用傳統算法訓練網絡，再采用彈性算法與BP網絡結合的改進算法，網絡訓練誤差曲線如圖3、圖4所示。
彈性算法不僅加快了收斂速度，防止了震蕩，還避免了陷入局部極小值，從圖3和圖4可以看出，通過彈性算法與BP網絡相結合以后，訓練次數由原來的769次減少到11次，大大提高了神經網絡的訓練效率。用樣本自身數據輸入訓練好的神經網絡中，識別結果見表4。與故障模式對比分析可知，自身檢測結果已經達到要求，即該網絡已經訓練好。下面檢測網絡的泛化能力，任取2組測試數據并進行歸一化處理，結果如表5所示。
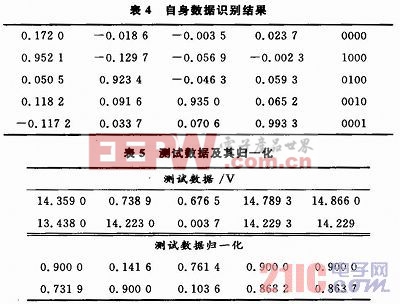
將歸一化的數據作為神經網絡的輸入，得到測試數據的識別結果，如表6所示。
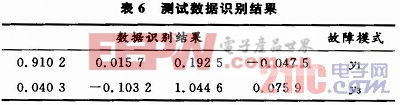
與故障模式對比可知，第一組對應的故障是R2短路，第二組對應的故障是R1開路。由此可以看出，訓練好的網絡不僅可以識別樣本自身故障，而且還具有一定的泛化能力，經過彈性算法與BP網絡的結合，取得了良好的效果，達到了預期的目標。
5 結語
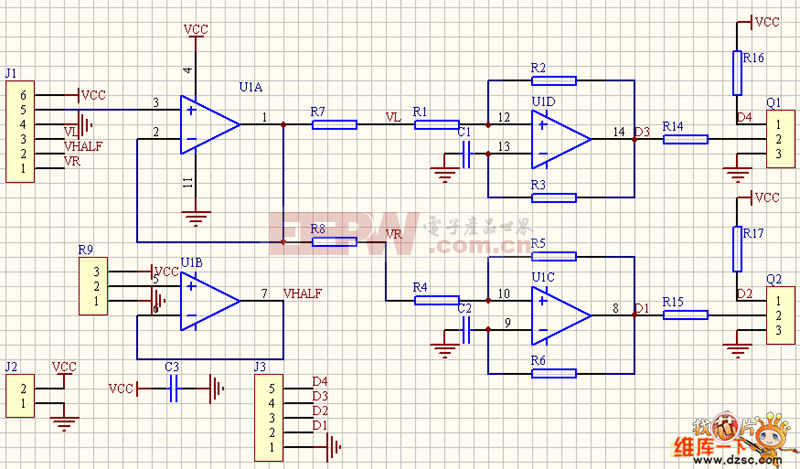
本文針對傳統BP算法誤差下降緩慢，調整時間長，甚至陷入局部極小點而不能自拔等局限性，運用彈性算法與BP網絡相結合的方法，結合某型雷達設備中的射頻放大電路進行建模、仿真，用Matlab設計并用改進后的算法訓練BP神經網絡，仿真結果證明該方法對克服傳統BP算法的局限性有顯著效果，縮短了網絡的訓練次數，提高了訓練效率，且診斷結果良好，為新型雷達裝備的故障診斷提供了一種有效的方法，在對裝備故障診斷維修上具有一定的實用意義。
評論