正確理解時鐘器件的抖動性能

摘要

在選擇時鐘器件時，抖動指標是最重要的關鍵參數之一。但不同的時鐘器件，對抖動的描述不盡相同，如不帶鎖相環的時鐘驅動器有附加抖動指標要求，而帶鎖相環實現零延時的時鐘驅動器則有周期抖動和周期間抖動指。同時，不同廠家對相關時鐘器件的抖動指標定義條件也不一樣，如在時鐘合成器條件下測試，還是在抖動濾除條件下測試等。

為了正確理解時鐘相關器件的抖動指標規格，同時選擇抖動性能適合系統應用的時鐘解決方案，本文詳細介紹了如何理解兩種類型時鐘驅動器的抖動參數，以及從鎖相環輸出噪聲特性理解時鐘器件作為合成器、抖動濾除功能時的噪聲特性。

1 概述

隨著半導體工藝速度和集成度的提高，以及模擬集成電路設計能力的提升，鎖相環芯片的產品形態越來越豐富，大大提升了系統時鐘方案設計的靈活性，同時降低了系統時鐘方案總成本。目前，鎖相環集成芯片已被廣泛應用于無線通信、數據網絡、消費電子、醫療設備和安防監控等領域，可以實現通信網定時同步、時鐘產生、時鐘恢復和抖動濾除、頻率合成和轉換、時鐘分發和驅動等功能。

面對時鐘器件供應商提供的種類繁多的芯片，為系統設計選擇滿足性能規格，同時總體方案成本又具有競爭力的時鐘電路，是電路設計者面臨的一個難題。由于時鐘器件的關鍵指標是抖動規格，高性能的抖動指標往往價格也要高很多，本文從分析時鐘器件的抖動規格入手，詳細介紹了如何正確地理解在時鐘芯片器件手冊里該指標的含義。基于抖動指標，介紹了德州儀器(TI)所提供的一系列時鐘器件及其抖動性能，幫助電路設計者選擇最適合自己的時鐘方案。

2 時鐘抖動和鎖相環噪聲模型

對時鐘器件而言，抖動和鎖相環是兩個最基本的概念。

2.1 抖動

如圖1 所示，時鐘抖動可分為三種抖動類型：時間間隔誤差TIE(Time Interval Error)、周期抖動PJ(Period Jitter)和相鄰周期間抖動CCJ(Cycle to Cycle Jitter)。周期抖動是多個周期內對時鐘周期的變化進行統計與測量的結果，相鄰周期間抖動是時鐘相鄰周期的周期差值進行統計與測量的結果，由于這兩種抖動是單個周期或相鄰周期的偏差，表征的是短期抖動行為。時間間隔誤差又稱為相位抖動(Phase Jitter)，是指信號在電平轉換時，其邊沿與理想時間位置的偏移量，通常表征的是長期抖動行為。

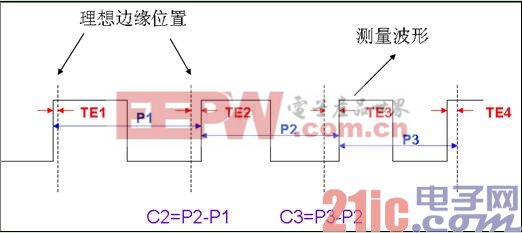
圖1 抖動定義

從時鐘抖動的來源分析，可以把抖動歸納為兩大類：確定性抖動和隨機性抖動。確定性抖動是由可識別的各種干擾信號造成的，如EMI 輻射、電源噪聲、同步切換噪聲等等，這種抖動幅度是有邊界的，而且可以通過電路設計優化把干擾源消除或大幅降低，一般是不直接描述時鐘器件的抖動性能。隨機抖動是不能預測的噪聲源，如熱噪聲(也稱為Johnson 噪聲或散粒噪聲)，以及半導體加工工藝的局限性等。由于隨機噪聲是由多種不相關噪聲源疊加的， 根據統計理論可以用高斯分布來描述其特性，由此可以得到下面兩種對隨機抖動幅度的表征：

1. 均值(RMS)抖動，即高斯分布一階標準偏差值。一般采用在規定的濾波器帶寬內的RMS 抖動，如光通信領域常用的積分帶寬是(12KHz ~ 20MHz)。

2. 峰峰值(Peak-to-peak)抖動，即高斯正態曲線上最小測量值到最大測量值之間的差值。根據數據系統誤碼率要求的不同，最小和最大值的取值是不一樣的，如誤碼率為 時，峰峰值約等于14 倍的標準偏差值，即為 。

2.2 相位噪聲

相位噪聲是對時鐘信號噪聲特性的頻域表征方式，表征時鐘信號頻率的穩定度，是指偏離載波頻率(f-fc)處1Hz 帶寬內噪聲功率與載波信號總功率的比值，符號為L(f)，單位為dBc/Hz。圖2 是一個時鐘信號的頻譜特性，如果單頻信號非常穩定的話，從頻譜上看其邊帶會隨著遠離主頻的位置逐漸降低，在偏離載波(f-fc)處，相位噪聲約等于載波頻率處曲線的高度與f 處曲線的高度之差，即圖中L(f-fc)

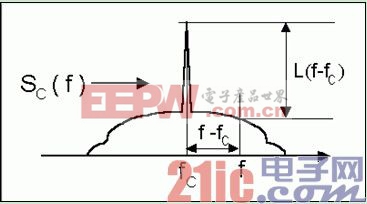
圖2 相位噪聲定義

2.3 均值抖動和相位噪聲關系

通過前面分析，噪聲可以用時域的相位抖動指標和頻域的相位噪聲指標來表征，但兩者反映了是同一個物理現象，故均值抖動可以通過頻域的相位噪聲曲線計算獲得，根據相關文獻，頻域的相位噪聲與均值抖動之間的關系如下式：

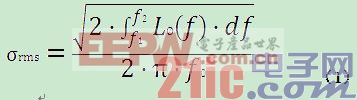
注：f1 和f2 為抖動積分上、下限頻率，f0 為信號中心頻率。

下面通過一個具體例子說明頻域的譜密度曲線如何轉換為時域的抖動值。

圖3 是某個鎖相環時鐘器件輸出的相位噪聲，載波頻率Vo= 156.25MHz，為計算方便，把相位噪聲曲線近似為圖中紅色曲線段，AB 和CD 段為常數 dBc/Hz，BC 段20dBc 衰減，冪率近似為 的噪聲類型。

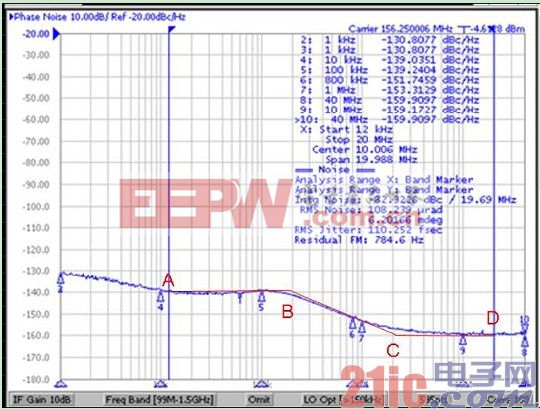
圖3 相位噪聲曲線

按照式子(1)關于相位噪聲與均值抖動間的轉換關系，去積分頻率取值范圍為12KHz ~ 20MHz，則：

2.4 鎖相環噪聲模型

圖4 是典型的鎖相環輸出噪聲分布特性曲線。在鎖相環環路帶寬內，主要噪聲成份是參考時鐘噪聲、分頻器噪聲、PFD 和電荷泵噪聲等;在環路帶寬外，主要噪聲源來自本地振蕩器VCXO/VCO。