削峰填谷最優(yōu)時(shí)基于DSM分時(shí)電價(jià)的確定與分析
作為用戶(hù)側(cè)電價(jià)的一種,分時(shí)電價(jià)目前在世界各國(guó)得到了廣泛的應(yīng)用,而且分時(shí)電價(jià)是需求側(cè)管理(DSM,Demand Service Management)的一種重要手段。分時(shí)電價(jià)可以刺激和鼓勵(lì)用戶(hù)主動(dòng)改變消費(fèi)行為和用電方式,達(dá)到削峰填谷的目的,從而提高電力系統(tǒng)的運(yùn)行效率和穩(wěn)定性。建立削峰填谷最優(yōu)時(shí)基于DSM分時(shí)電價(jià)的數(shù)學(xué)模型,利用數(shù)值仿真驗(yàn)證了該分時(shí)電價(jià)的削峰填谷作用,與文獻(xiàn)[5-6]仿真結(jié)果進(jìn)行了比較,得出了本文確定的分時(shí)電價(jià)的優(yōu)缺點(diǎn),對(duì)本文分時(shí)電價(jià)數(shù)學(xué)模型的應(yīng)用進(jìn)行了構(gòu)想。
關(guān)鍵詞:分時(shí)電價(jià);需求側(cè)管理;削峰填谷;數(shù)值仿真
Determination and Analysis of TOU (Time-Of-Use) Power Price Based on DSM (Demand Service Management) When Load Shifting Optimized
Wu Qiu-wei1,Wang Lei2, Cheng Hao-zhong1
( 1. Department of Electrical Engineering Shanghai Jiaotong University 200030 2. Nanjing Power Supply Nanjing 210094)
Abstract: As one of power prices to consumers, TOU power price is widely used in the world and is one important method in DSM. TOU power price can motivate power consumers to adjust their mode of power using and can keep power load in a stable condition. Thus efficiency and stability of power systems can be improved. In this paper a new mathematical model of TOU power price is developed when effect of load shifting is optimized based on DSM. Numerical simulation is made using MATLAB. It is verified that using TOU power price in this paper can accomplish the goal of load shifting. Merits and defects of TOU power price determined in this paper are obtained by comparing with simulation results in paper 5 to paper 6. Realistic application of TOU power price mathematical model is forecasted.
Keywords: TOU power price DSM load shifting numerical simulation
0 引言
電價(jià)理論是電力市場(chǎng)的核心理論[1]。在電力市場(chǎng)環(huán)境下,確定合理的用戶(hù)側(cè)電價(jià),可以使用戶(hù)積極參與電力工業(yè)改革,調(diào)整用電方式和用電結(jié)構(gòu),使負(fù)荷保持在一個(gè)比較平穩(wěn)的狀態(tài),提高電力系統(tǒng)運(yùn)行效率和穩(wěn)定性。作為用戶(hù)側(cè)電價(jià)的一種,分時(shí)電價(jià)目前在世界各國(guó)得到了廣泛的應(yīng)用,而且分時(shí)電價(jià)是需求側(cè)管理的一種重要手段。在我國(guó),DSM和分時(shí)電價(jià)也得到了廣泛的研究。文獻(xiàn)[2]和[3]認(rèn)為我國(guó)目前實(shí)行實(shí)時(shí)電價(jià)的條件不具備,但實(shí)行分時(shí)電價(jià)是必不可少的。文獻(xiàn)[4]主要針對(duì)江蘇省實(shí)行分時(shí)電價(jià)后大工業(yè)用戶(hù)的響應(yīng)進(jìn)行了分析,認(rèn)為實(shí)行分時(shí)電價(jià)具有一定的負(fù)荷調(diào)節(jié)效果。文獻(xiàn)[5]提出了用戶(hù)反應(yīng)的概念來(lái)描述電價(jià)對(duì)負(fù)荷的影響,并提出了基于DSM的分時(shí)電價(jià)的數(shù)學(xué)模型,但它們均未涉及平時(shí)段電價(jià)的確定問(wèn)題。文獻(xiàn)[6]對(duì)平時(shí)段電價(jià)的確定進(jìn)行了探索性研究,提出了用MCP計(jì)算的平均購(gòu)電電價(jià)來(lái)確定平時(shí)段電價(jià),將文獻(xiàn)[5]的工作拓廣到與電力市場(chǎng)報(bào)價(jià)端相關(guān)聯(lián)的模型研究,從一個(gè)可行的途徑將分時(shí)電價(jià)市場(chǎng)化,得到適應(yīng)電力市場(chǎng)條件的分時(shí)電價(jià)體系。但是,由于MCP對(duì)平時(shí)段電價(jià)的限制,文獻(xiàn)[6]確定的分時(shí)電價(jià)不能得到使削峰填谷最優(yōu)的平時(shí)段電價(jià)。從電力系統(tǒng)角度來(lái)考慮,要盡可能地減小峰負(fù)荷和提高谷負(fù)荷,這樣才能最大可能地提高電力系統(tǒng)運(yùn)行效率和穩(wěn)定性。因此,本文對(duì)削峰填谷效果最優(yōu)時(shí)分時(shí)電價(jià)的確定進(jìn)行了研究,提出了削峰填谷效果最優(yōu)時(shí)分時(shí)電價(jià)數(shù)學(xué)模型,利用MATLAB進(jìn)行了數(shù)值仿真,驗(yàn)證了該數(shù)學(xué)模型確定的分時(shí)電價(jià)的削峰填谷作用,并與文獻(xiàn)[5-6]仿真結(jié)果進(jìn)行了比較,得出本文確定的分時(shí)電價(jià)的優(yōu)缺點(diǎn)。
1 基于DSM與用戶(hù)購(gòu)電費(fèi)用的分時(shí)電價(jià)數(shù)學(xué)模型
本文仍采用文獻(xiàn)[6]中用戶(hù)反應(yīng)定義和數(shù)學(xué)模型描述電價(jià)對(duì)負(fù)荷的控制作用。
1.1 基本假設(shè)與參量的設(shè)定
1.1.1 基本假設(shè)
(a) 實(shí)行分時(shí)電價(jià)前后每天的總用電量保持不變。
(b) 調(diào)整到某一時(shí)段的電量按時(shí)間軸平均分配。
(c) 文中只考慮了價(jià)格對(duì)用戶(hù)需求的影響,其他因素的影響需進(jìn)一步研究;同樣文中只考慮了用戶(hù)需求對(duì)價(jià)格的影響,其他因素(如燃料價(jià)格)對(duì)價(jià)格的影響暫時(shí)忽略。
根據(jù)國(guó)外實(shí)行需求側(cè)管理的經(jīng)驗(yàn),在實(shí)行需求側(cè)管理后,一般用電量略有增加或基本保 持不變,因而假定實(shí)行分時(shí)電價(jià)前后用電量保持不變是合理的。與[4-6]一樣,假設(shè)(b)、尤其是假設(shè)(c)是為了使本文的討論得以順利進(jìn)行所作的簡(jiǎn)化性假設(shè),特別的消除假設(shè)(c)是一個(gè)十分重要的問(wèn)題,有待進(jìn)一步的研究。
1.1.2 參量的設(shè)定
1) 時(shí)段的劃分
我們將一天24小時(shí)劃分為3類(lèi)時(shí)段:Tf、Tp、Tg,滿(mǎn)足:
Tf+Tp+Tg=24 (1)
其中:Tf峰時(shí)段;Tp平時(shí)段;Tg谷時(shí)段
在本文中,我們假定時(shí)段劃分確定,根據(jù)負(fù)荷曲線中負(fù)荷的分布來(lái)進(jìn)行時(shí)段劃分。時(shí)段劃分的具體數(shù)值為:
峰負(fù)荷時(shí)段:8:00~12:00(峰1),18:00~22:00(峰2);平負(fù)荷時(shí)段:12:00~18:00(平1),22:00~24:00(平2);谷負(fù)荷時(shí)段:0:00~4:00(谷1),4:00~8:00(谷2)。
2) 電價(jià)的確定
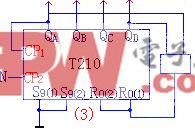
峰、平、谷時(shí)段的電價(jià)分別為:Pf、Pp、Pg。滿(mǎn)足:

其中:Δ 為谷時(shí)段電價(jià)對(duì)平時(shí)段電價(jià)的拉開(kāi)度;ξ為峰時(shí)段電價(jià)對(duì)平時(shí)段電價(jià)拉開(kāi)度與谷時(shí)段電價(jià)對(duì)平時(shí)段電價(jià)拉開(kāi)度的 比值。
3) 用電量
某負(fù)荷代表日的負(fù)荷曲線為L(zhǎng)=L(t)(0≤t≤24),則:
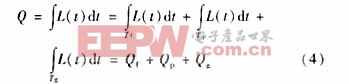
其中:Q全天用電量;Qf 峰時(shí)段的用電量;Qp為 平時(shí)段的用電量;Qg為 谷時(shí)段的用電量
1.2 分時(shí)電價(jià)數(shù)學(xué)模型
本文根據(jù)DSM的總體目標(biāo)和經(jīng)濟(jì)學(xué)中的會(huì)計(jì)學(xué)原理,從供需兩側(cè)出發(fā)建立了分時(shí)電價(jià)模型。
1) 供方獲利
實(shí)行分時(shí)電價(jià)前供電方的銷(xiāo)售收入為:
![]()

其中:QfTOU、QpTOU、QgTOU為實(shí)行分時(shí)電價(jià)后峰、平、谷時(shí)段的用電量
實(shí)行分時(shí)電價(jià)后供電方通過(guò)削峰可以節(jié)約的電力建設(shè)投資為M′。
供電方獲利的約束條件是:![]()
2) 用戶(hù)端受益
即
3) 優(yōu)化目標(biāo)
盡可能減小峰負(fù)荷,提高谷負(fù)荷,從而提高電力系統(tǒng)的負(fù)荷率、電力系統(tǒng)的運(yùn)行效率和穩(wěn)定性,并且盡可能減少用戶(hù)購(gòu)電費(fèi)用,從而達(dá)到社會(huì)效益最優(yōu)的目的。因此,目標(biāo)函數(shù)為:
目標(biāo)函數(shù)1: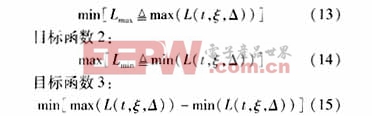







評(píng)論