完美無諧波高壓IGBT變頻器

1前言

國外某公司利用一種新的高壓變頻技術，生產出功率為315kW～10000kW的完美無諧波高壓變頻器（PERFECTHARMONY），無需附加輸出變壓器實現了直接3kV或6kV高壓輸出；首家在高壓變頻器中采用了先進的IGBT開關器件；達到了完美的輸入輸出波形，無需附加任何濾波器就可以滿足各國供電部門對諧波的嚴格要求；輸入功率因數達到095以上；總體效率（包括輸入隔離變壓在內）高達97％。達到這樣高指標的原因是因為采用了三項新的高壓變頻技術：一是在輸出逆變器部分采用了具有獨立電源單相橋式SPWM逆變器的直接串聯疊加；二是在輸入整流部分采用了多相多重疊加整流技術；三是在結構上采用了功率單元模塊化技術。

2單相橋式SPWM逆變器的直接串聯疊加

單相橋式SPWM逆變器的直接串聯疊加法，是通過N個具有獨立直流電源的單相橋式SPWM逆變器直接串聯的方式級聯而成的，這是專為高壓大功率逆變器使用的一種串聯疊加法。此法是用N個依次移開2π/N相位角的載波三角波，與同一個正弦調制波進行比較產生出N組控制信號，用這N組控制信號（N組信號依次相差2π/N相位角）去依次控制N個具有獨立直流電源的單相橋式SPWM逆變器，使每一個單相橋式逆變器輸出相同的基波電壓，然后將N個單相橋式逆變器的輸出電壓串聯起來，就可以得到多電平SPWM無諧波電壓輸出，這種串聯不存在均壓問題。

21兩個單相橋式SPWM逆變器的串聯疊加

現個具有獨立直流電源單相橋式SPWM逆變器的直接串聯疊加電路如圖1所示。由于N=2，所以載波三角波的移相角α==π(=180°)。對于三相輸出逆變器來說，其A相電路由兩個單相橋式SPWM逆變器A1和A2串聯組成。A1的載波三角波的移相角α=0；A2的載波三角波的移相角α=(=180°)。A1和A2的載波三角波用同一個A相的正弦波進行調制。這樣就可以得到A1的輸出電壓up1、A2的輸出電壓up2。up1和up2具有相同的基波電壓。A1和A2串聯后的輸出電壓uA=up1＋up2就是輸出為正弦波的無諧波電壓、其波形如圖2所示。

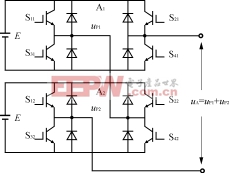
圖1兩個單相橋式SPWM逆變器的串聯疊加

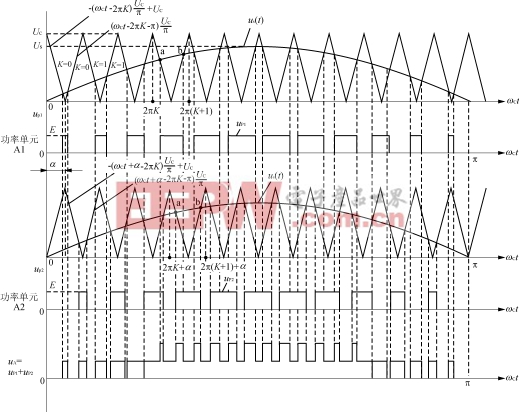
圖2A1及A2串聯疊加后的波形

為了求出單相橋式SPWM逆變器A1、A2的輸出電壓up1、up2的SPWM波形，必須先求出SPWM波形中各脈沖前、后沿a、b點的座標，為此先列出載波三角波的方程式：

對于單相逆變器A1α=0

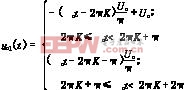（1）

對于單相逆變器A2α=180°（2）

K=0，±1，±2…

調制波的方程式為：us(t)=Ussinωst（3）假定載波比，調制比。

對于單相逆變器A2的輸出電壓up2的波形，

在采樣點a：Ussinωst=－

令ωst=Y；ωct=X，

則X=2πK＋π－α－πMsinY

在采樣點b：X=2πK＋π－α＋πMsinY

從圖2中A2的up2波形可知：X=ωct在2πK＋α到2π(K＋1)＋α區間內，在a、b點之間得到up2的正脈沖，故可以得到up2的SPWM波的時間函數式為：up2(X，Y)=(4)Y=X

函數up2(X，Y)可以用雙重付里葉級數表示：up2(X，Y)=Aoo＋(AoncosnY＋BonsinnY)＋(AmocosmX＋BmosinmY)＋{Amncos(mX＋nY)＋Bmnsin(mX＋nY)}

式中：Amn＋jBmn=up2(X，Y)

將式（4）代入上式得：Amn＋jBmn==

由貝塞爾函數得：所以：Amn＋jBmn=

·〔〕=j(5)

當n為零或偶數時，=0，Amn＋jBmn=0，

當n為奇數時，=2所以：Amn＋jBmn=jJn(mMπ)

·〔cosm(π－α)＋jsinm(π－α)〕Amn=－Jn(mMπ)sinm(π－α)；Bmn=Jn(mMπ)cosm(π－α)當m=0時=1Aon＋Bon=up2(X，Y)

因為up2(X，Y)是奇函數，故得：

Aon=0Bon=up2(X，Y)=

當n=1時，Bo1=ME；當n≠1時，Bon=0

故得up2的SPWM波形的雙重付里葉級數式為：up2(t)=MEsinωst＋cosm(π－α)·sin〔(mF＋n)ωst〕－sinm(π－α)