DC－DC開關變換器中混沌現象的研究綜述

3.3 數值仿真法

數字仿真是指利用各種各樣的算法以求得變換器某些特性數字解的方法。它分為直接數字仿真法和間接數字仿真法兩種。數字仿真的優點是準確度和精確度都高，可以得到響應的完整波形;適用范圍廣，可進行小信號分析和大信號分析。

由于混沌動力學系統的復雜性，很多混沌動力學系統不能用已知函數表示其通解，使得解析法很多時候無能為力，而且用解析法建模時，常常需要作出某些近似，以簡化分析。眾所周知，開關調壓系統存在著功率級電路的開關非線性和控制電路中脈沖調制器的飽和非線性，因此不能用精確方法設計電路，也難以用解析法對混沌類現象進行有效的預測，同時這類系統受到的擾動常常是大幅度的，這時系統在大信號擾動下工作，對于大信號分析，一般很難用解析法求解，更需要借助于數字仿真，從而這就使通過數值計算來描述混沌行為的演化過程對開關變換器的混沌進行數值模擬顯得十分重要[11]。

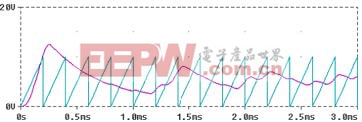
下面以PWM型BUCK變換器為例，用PSPICE對其進行仿真。如圖，假定電路中的器件均是理想的，電路中參考電壓Vref輸入至反相器的反相端，R上的電壓V(t)輸入至誤差放大器OA1的正向輸入端，OA2的正向端為一個時鐘信號——鋸齒波電壓，放大器產生一個控制信號，作用于PWM，與時鐘信號比較。每周期初始，PWM輸出脈沖，當反饋電路的輸出端(即控制電壓)高于鋸齒波電壓時，輸出為高電平，壓控開關導通;當鋸齒波電壓上升到控制電壓時，輸出脈沖截止。直到下一周期開始，再次輸出脈沖。因此控制電壓的波形決定了輸出脈沖的寬度，進而決定了開關管的導通時間。這樣產生一系列的脈沖信號來控制主電路的壓控開關的。電路中的參數值如下： 輸入電壓Vs=10v ，電容C=100uf，電感L=100uh，負載電阻R=22， 參考電壓Vref=5v，鋸齒波電壓Vpulse(0v，10v，0s，199.99u，0.005u，0.005u，200u)，放大器的放大倍數e=15，穩態時，變換器的輸出含周期性的紋波，然而某些情況下，電路會發生多脈沖現象，開關通斷多次，從而增加了開關損耗，變換器的效率降低。我們用PSPICE仿真后可得，如下圖：

4 穩定性及穩定條件

一般的，穩定的DC—DC變換器表現為周期性的穩態。一旦初始暫態值衰減，狀態變量就以周期重復。控制相應的離散系統的映射有一個吸引性固定點：在周期性的穩態，每一個周期都與下一個相同，所以在每個周期采樣得到的情況都一樣。若變換器是局部漸近穩定，相應的一個小的擾動它會使周期穩定下來，這個離散系統相應的序列會收斂于這個固定點，因此，這個點是吸引子。相反，若變換器初態是不穩定的，這個序列會偏離固定點。因此，可以得出結論：映射的固定點的穩定性決定連續系統的局部穩定性。一個吸引性的固定點對應著連續系統的周期性的穩態。

一階系統穩定的條件是映射在固定點處的梯度在-1和1之間。 即

固定點的穩定性也可以推廣到高階。不同的是，一階的穩定性由梯度決定，而高階由特征增益率決定，固定點的特征增益率是映射在固定點處的雅可比陣的n個特征值。其中雅可比陣是對各個元素求X偏導后所得矩陣。高階系統穩定的條件是若特征增益率都落在復平面上的單位圓之內，則固定點穩定。

5 混沌的研究狀況

因為分叉、混沌等不穩定現象與系統的非線性密切相關，所以在分析研究時必須跳出線性電路的范疇[12].目前最常用的方法是一維映射法。一般的，開關變換器的離散表達式

可寫作

，其中

為輸入,

是第N個周期的占空比, F、T分別是系數矩陣的指數函數。對于閉環工作的開關變換器，一般有

，

是非線性函數，因而

，這就是一維映射法的原理[13].現在已有比較成熟的理論。文獻[10，5，14]使用該法分析了電流反饋的變換器的分叉混沌現象。最近，Tse的一系列工作如[15]都是推導出該一維映射的解析表達式，通過研究這一映射來得到變換器的動力學性質，揭示了變換器從倍周期、分叉走向混沌的具體過程。

另外，從國內外的研究工作來看，各種頻繁出現在其他領域的線性或非線性現象，都可以在開關變換器中找到類似情況。開關變換器中的混沌運動同樣也與周期軌道有密切關系，在分叉參量變化過程中，閉環系統的變換器往往先以各種方式經歷一系列周期、倍周器、準周期事件，最后才進入混沌狀態，這通常稱為通向混沌的具體道路。文獻[6]從計算機模擬和實驗兩方面驗證了開關變換器不僅在PWM閉環時會產生混沌，即使在開環情況下，由于二極管和晶體管等開關功率元件的非線性極間電容影響，變換器仍可能產生混沌。文獻[16]研究了電流控制型變換器中的輸入電壓，電容電感以及開關頻率等參數對系統分叉、次諧波、混沌等不穩定行為的影響，并畫出了穩定區域和不穩定區域。目前，不穩定的分析方法還不完善。文獻[17]用微分動力系統方法研究了Boost變換器的分叉現象，認為該電路存在靜態分叉和動態分叉并得出其存在的條件。雖然文獻[17]的方法處理嚴格，結果較為準確，但是較繁瑣。

6 結束語

本文對變換器的混沌概念、特點、分析方法、研究現狀作了一個較全面的綜述。由上可知，隨著混沌理論的發展，變換器中的混沌現象的研究也有了一定的成果。，混沌的分析方法還主要是一維映射法，但是一維映射法是否適合于所有的變換器，是否還有別的方法，這都有待進一步研究。