DC－DC開關變換器中混沌現象的研究綜述

1 引言

從非線性動力學角度來說，開關變換器是一個強非線性時變動力學系統，因此存在著豐富的非線性現象，包括各種類型的次諧波、分叉與混沌等。由于混沌動態是一種不穩定振動，混沌現象是一種不正常不可靠的現象，混沌的不確定性將導致系統的運行狀態無法預測，從而使變換器的控制性能受到極大的影響，甚至完全不能工作，所以研究開關變換器中混沌產生的方式、分析方法有助于我們在設計中避開這種不理想現象，使變換器工作于穩定的周期，這對于正確設計和調試開關變換器具有重要的指導意義。

本文對混沌的國內外研究現狀作一綜述，并詳細介紹其分析方法。

2 混沌的基本概念

1963年，Lorenz從簡化的大氣模型中推導出著名的Lorenz方程，這組三階的微分方程呈現出一種奇異的現象，即混沌現象，從此揭開了混沌學發展的新篇章。Lorenz微分方程組如下：

(1)

在這個系統中，S ，R，B是可變參數，其中任意參數的改變都可能導致系統從周期態向混沌態的轉變[1]。

從Lorenz系統中研究可知，產生混沌的原因是耗散和非耗散相互作用的結果。耗散作用的整體穩定性和非線性作用的局部不穩定性作用便形成了混沌[2].而奇異吸引子是混沌的本質所在。這時候人們發現即使對于典型的可用確定論方法描述的系統來說，只要該系統稍微復雜一些，在一定條件下也會產生非周期的表面上看起來毫無規律的運動，改變了那種認為用確定論方法描述的運動都屬于規則運動的錯誤觀念。這種來自可用確定論方法描述的系統中的無規則運動，稱為混沌或內在隨機性。它表面上是隨機運動，實際上是有一定結構的形式，而真正的隨機行為出現在嘈雜系統中。混沌運動通常還具有確定性運動所沒有的特征，如局部不穩定而整體穩定、無限自相似、對初值變化的高度敏感性、奇異吸引子中包含多個不穩定周期軌道、連續的功率譜等[3]。首次證明開關變換器中存在混沌的是Brockett和Wood，他們在1984年發表的一篇會議論文中指出受控的Buck 變換器可產生混沌行為[4]。1988年，Hamill和Jefferies首先對開關變換器中的混沌現象進行了理論分析[5]。而文獻[6]指出由于開關變換器是強非線性離散系統，而非線性微分方程的解不是唯一的，當非線性系統的周期解處于臨界狀態時，它對微小的參數攝動或初始條件變化都極為敏感，就可能進入連續分頻狀態，最后出現混沌。

3 混沌的分析方法

Middlebrook等在1976年提出的狀態空間平均法[7]是目前使用最廣泛的方法。它將時變電路變成了非時變線性電路，從而可求穩態工作點、小信號傳遞函數等。它是簡明性和準確性的一個較好的折中。但也存在著穩定性分析不準確、不能分析紋波、無法分析準諧振變換器等缺點。另外，它在連續導電模式中忽略了開關變換器頻率的影響，由此而產生的線性模型中，占空比成為連續的時間變量，然而實際上占空比是定義成離散時間變量的，在一個開關周期內討論占空比的變化是毫無意義的[8].由于所得到的是一個線性模型，忽略了開關變換器的非線性特征，因此不可能對開關變換器中的次諧波、混沌等非線性現象作出正確的分析，這些不足使得離散時間模型[9]應運而生。它保留了變換器的非線性特性，是較為準確的一種方法，一般可以得到映射的隱式表達。它的主要特點是提出采樣序列的概念，而不是把開關描述成連續的，即每隔一定時間對變換器作一次采樣，通常是在波峰波谷處采樣更方便。開關周期內狀態的變化由一映射函數描述。這個函數可能會較復雜，但一旦得到，就可以用計算機來對它進行反復迭代，從而確定變換器的狀態是怎樣從一個周期演變到另一個周期的。

文獻[10]是基于離散時間模型的非線性迭代映射法。一般的，其狀態方程可以描述為

=f(x，t)，其中x是n維狀態矢量(常為電容電流或電感電壓)，每一個周期對X采樣(通常在波峰或波谷處)，即可得到一個離散系統。于是就得到一個{

}序列，時間就不出現在方程里了。

3.1 一維映射

對于一維映射 x——>F(x)， F是一個作用在一個實數上來產生另一個實數的函數。滿足方程x*=F(x*)且在映射下保持不變的點叫F的固定點。我們的興趣在于用這個函數將一個區域劃到它自己內部。例如x—>ax(1-x)， 其中a是一個參數，0≤a≤4，這個函數就是將區間[0，1]劃到它內部。若a=2，則方程變為

m=0，1，2

這是一個一階差分方程，x的當前值僅由前一個值決定。從任一個初值

開始反復迭代就可以得到一個序列{

}.任選一個不等零的初值，序列最終收斂于x*=0.5，這個點叫做吸引性固定點。反之對于固定點x*=0，若初值不等零，而序列會偏離初值，則這個點不具有吸引性。 由上可知，固定點對系統有著重要影響。 特別的，穩定行為與吸引性固定點有關系。，那樣的點叫穩定固定點。而不具有吸引性的固定點會導致混沌。

3.2 高維映射

迭代法對高維映射也適用。在n維情況下，令人關注的是n維矢量之間的關系。這時候，F作用在一個矢量上以產生另一個n維矢量。與一維映射同樣，我們的興趣在于把一個區域劃到它內部，不同的是這個區域是一個n維空間.下面給一個二維例子,

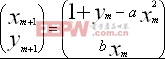
(2)

其中x=

, a、b均是參數。因為必須把函數畫在二維空間里,所以要看高維映射是較困難的,甚至n =2這種情況也不例外。同樣，對于高維映射，滿足

的矢量

即為固定點。如當 a=1.4、b=0.3時,方程(2)有兩個固定點,但都不具有吸引性,因而會導致混沌。