數字語音混沌保密通信系統及硬件實現
加入技術交流群
混沌序列在密碼學方面的應用起源于80年代末期，由英國數學家Matthews首先提出[1]，其后得到了一定的發展。國內南京大學聲學研究所的倪皖蓀、中國科學院的張洪均等也正在進行這方面的研究工作。
基于混沌系統之間能夠達到自同步[2]，發展了多種同步技術，如：混沌掩埋技術[3]、混沌調制技術[4]、混沌開關技術[5]以及數字混沌通信技術[6]等，分別運用于連續混沌通信系統和數字混沌通信系統。眾所周知，數字通信系統以其抗干擾能力強，易于加密，易于大規模集成等特點，在通信行業中將取代模擬通信而占主要地位。而且，數字混沌系統比較模擬混沌系統具有結構簡單，易于實現，保密性能高等優勢。因而，混沌技術在數字保密通信中的應用研究也就更具有現實意義。
本文對離散時間動力學系統邏輯影射進行變換，使其在一定精度下產生數字混沌序列，采用該數字混沌序列作為密碼，構造了語音保密通信系統，并運用單片機實現了該系統的硬件實驗。
1 數字混沌序列的產生
研究證明邏輯映射
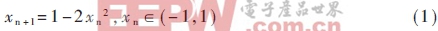
可以產生大量具有均值為零、自相關為δ函數、互相關為零統計特性的優良混沌序列，因而可作為理想的密碼序列，應用于語音信號的保密傳輸。
要實現邏輯映射的數字化，一種方法是采用浮點運算。實際運算表明，浮點單精度(32bit)的運算結果脫離了混沌態，浮點雙精度(64bit)的運算結果與理論接近。但在實際應用中，64bit浮點雙精度運算需要內存空間大，運算速度慢，而且不利于數字硬件實現。下面我們把邏輯映射的迭代過程由浮點運算變換為定點運算。
我們日常生活中普遍使用的十進制小數同計算機中使用的二進制存在如下關系：
其中：，
從(3)式可知，X為一十進制整數，它是由一個十進制小數映射而來，而十進制整數在計算機中可用定點整數形式來表示。
我們將(3)式代入邏輯映射(1)可得：
這就是邏輯映射的整數表達式。在作者即將發表的另一篇文章中，對L為64位、32位和16位分別進行了計算機編程模擬，證明當L＝32時，式(5)產生的序列仍然處于混沌態(而同樣32bit條件下，采用浮點運算得不到混沌序列)。當L＝16時，式(5)產生的序列已經脫離了混沌態，但經過一定的非線性變換仍可產生混沌序列，對式(5)進行微小的改動(即非線性變換)為：
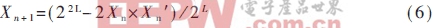
其中Xn＝(XnH)(XnL)，Xn′＝(XnL) (XnH)，即Xn′為Xn的高低字節互換后的16位二進制數。取L＝16比特根據式(6)產生數字混沌序列的流程圖如圖1所示。因此整數運算優于浮點運算，它降低了對計算精度的要求。產生L比特輸出，只需運算L×L比特定點運算，加快了計算速度，從而減低了對硬件電路的要求。
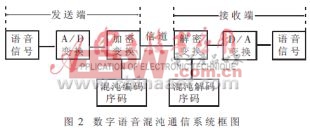
評論