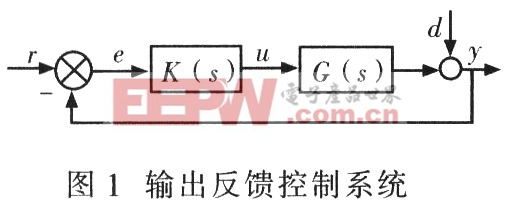
基于H∞混合靈敏度的導彈解耦控制器設計方法
加入技術交流群
3 耦合彈體的數學模型
由上述3個通道的簡化模型可知，偏航通道的彈體運動方程中含有滾動通道的參量(δ，γ)，滾動通道的彈體運動方程中含有偏航通道的參量(δ,ψ,β)。將相互耦合的俯仰一法向通道(1)，偏航通道(2)與滾動通道(3)聯立，組成兩輸入、兩輸出的多變量系統，取狀態向量為[β ψ ψ γ γ]T，控制輸入為u=[δψc δγc]T，測量輸出為r=[ψc γc]T，得到彈體運動方程的狀態空間表示為：
本文引用地址：http://www.104case.com/article/163432.htm △A,△B為高頻彈性振動等引起的參數不確定性部分，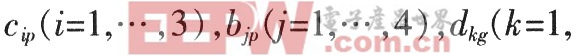
2，3,4)為系數。
由式(5)可知，S(s)+T(s)=I，I為單位陣。選擇適當的加權函數，對S(s)和T(s)進行頻域整形，即在低頻段以減小靈敏度函數的增益為主，而在高頻段以減小互補靈敏度函數增益為主，使系統頻域整形后滿足：
式中，Ws(s)為反映系統抗干擾的性能加權，WT(s)為反映系統魯棒性加權。
4．2 解耦控制器設計問題
由式(5)可知，T(s)為圖1所示系統的閉環傳遞函數。為此可以將T(s)成形為理想的對角矩陣來達到解耦的目的。文獻[4]給出將H∞混合靈敏度成形為標準的H∞問題，本文是在此基礎上加以推導，并選擇適當加權函數，達到解耦的目的。圖2為H∞混合靈敏度框圖。圖2中，z1，z2為性能評價輸出。uS，uT分別為Ws(s)和WT(s)的輸入，yG為G(s)的輸出。
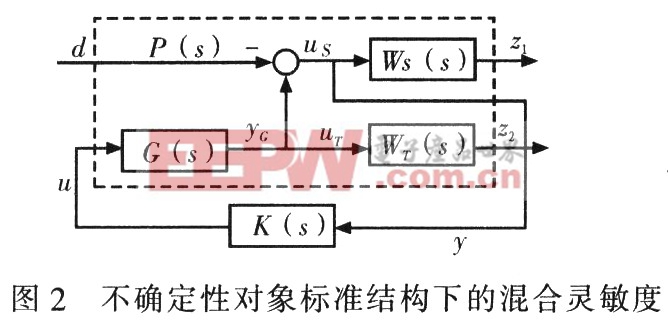
則G0(s)，WS(s)，WT(s)的狀態空間實現分別為：
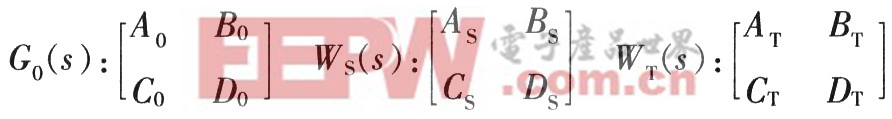
由圖2可知，系統P(s)的輸入為d,u，輸出為z1，z2，y。設x0，xS，xT為G(s)，WT(s)，WS(s)的輸出狀態。由圖2可以推導：yG=C0x0+D0uyuT=yg，us=d-yG，則：
評論