基于H∞混合靈敏度的導(dǎo)彈解耦控制器設(shè)計方法

1 引言
導(dǎo)彈在大攻角飛行過程中，通道間存在嚴重的氣動耦合。工程設(shè)計上，通常把較小的耦合項作為隨機干擾來處理，但當(dāng)耦合影響較大時，容易使控制系統(tǒng)喪失穩(wěn)定性，因此必須考慮通道間的耦合效應(yīng)，并對其解耦。近年來，隨著控制理論的發(fā)展，多種解耦控制方法應(yīng)運而生，如特征結(jié)構(gòu)配置解耦、自校正解耦、線性二次型解耦、奇異攝動解耦、自適應(yīng)解耦、智能解耦、H∞解耦，變結(jié)構(gòu)解耦等，其中文獻[4]采用多變量頻域法，將耦合的MIMO系統(tǒng)化為一系列的SISO系統(tǒng)，再用經(jīng)典頻域法分別設(shè)計，實現(xiàn)了BTT導(dǎo)彈自動駕駛儀的解耦，文獻[5]采用輸出反饋特征結(jié)構(gòu)配置方法，合理配置了閉環(huán)系統(tǒng)的特征值、特征向量，求取輸出反饋與前饋控制器，實現(xiàn)導(dǎo)彈三通道的解耦，文獻[6]利用變結(jié)構(gòu)控制和魯棒控制，實現(xiàn)系統(tǒng)的動態(tài)解耦。
根據(jù)導(dǎo)彈在大攻角飛行過程中，導(dǎo)彈受到的參數(shù)不確定性和外界干擾等都非常大，采用一般的解耦方法很難保證控制系統(tǒng)的實時性要求，由于H∞混合靈敏度自身優(yōu)點，這里提出了基于H∞混合靈敏度解耦控制器的設(shè)計方法。H∞混合靈敏度解耦控制器是將理想的無耦合的閉環(huán)系統(tǒng)參與到混合靈敏度設(shè)計中去，從而達到解耦的目的。在H∞混合靈敏度控制器設(shè)計中，需要進行權(quán)函數(shù)的選取，使其達到解耦目的。該解耦控制方法的優(yōu)點在于：由于H∞混合靈敏度控制器本身的優(yōu)點，使得該解耦控制器具有較強的魯棒穩(wěn)定性和抗干擾能力。

2 大攻角再入導(dǎo)彈簡化數(shù)學(xué)模型
導(dǎo)彈的動力學(xué)特性由一組非線性、變系數(shù)的方程組描述。由于存在彈性振動、液體晃動和發(fā)動機搖擺等因素的影響，該方程組非常復(fù)雜。為了對導(dǎo)彈運動方程的各種分析、計算和導(dǎo)彈控制系統(tǒng)設(shè)計提供方便，本文采用小擾動簡化措施。考慮導(dǎo)彈剛體運動和彈性振動，假設(shè)偏航、滾動通道標(biāo)準(zhǔn)彈道參數(shù)為零，即得到以下基于小擾動假設(shè)的彈體運動方程。小擾動彈體運動由剛性彈體姿態(tài)運動方程和彈性振動方程組成。式(1)～式(3)為簡化的數(shù)學(xué)模型。
(1)俯仰一法向通道剛體運動方程：

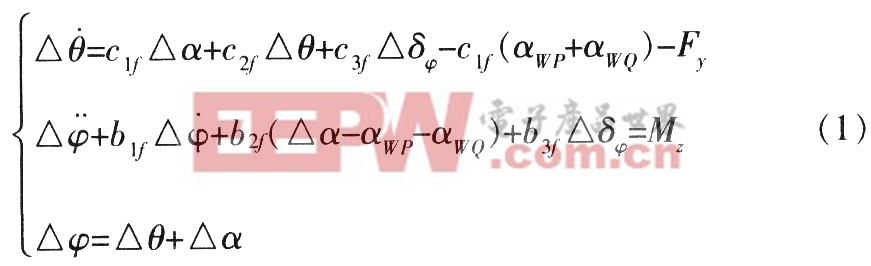
式中，αWP，αWQ分別為由于平穩(wěn)風(fēng)、切變風(fēng)作用形成的附加迎角；My，Mx為結(jié)構(gòu)干擾力矩；δ為彈道航向角；β為彈道側(cè)滑角；ψ為彈道偏航角；δψ為實際彈道偏航舵偏角；Fx為結(jié)構(gòu)干擾力。
(2)偏航一橫向通道剛體運動方程：

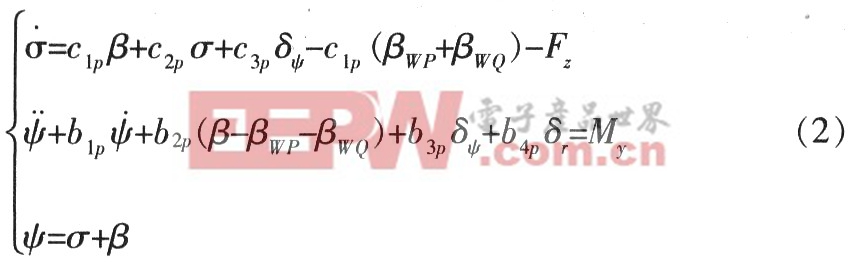
式中，βWP和βWQ分別為導(dǎo)彈由于平穩(wěn)風(fēng)、切變風(fēng)作用形成的附加側(cè)滑角；qiψ為偏航-橫向通道第i個振型(不包括剛體振型)所對應(yīng)的廣義坐標(biāo)。
(3)滾動通道彈體運動方程：

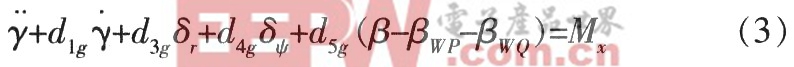
式中，γ為彈道滾動角；δr為彈道滾動舵偏角。