模糊滑模控制在蹺蹺板系統(tǒng)中的應(yīng)用研究
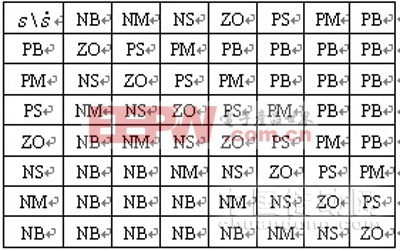
表中所有的控制規(guī)則是根據(jù)滿足 ![]() 這個達到滑模的充要條件所設(shè)計的[8],所以設(shè)計的模糊滑模控制系統(tǒng)是穩(wěn)定的。
這個達到滑模的充要條件所設(shè)計的[8],所以設(shè)計的模糊滑模控制系統(tǒng)是穩(wěn)定的。
4 仿真研究
定義S ,![]() , 其論域分別為
, 其論域分別為![]()
,![]() ,
,![]() ,模糊化變量均選擇正態(tài)分布隸屬函數(shù)。
,模糊化變量均選擇正態(tài)分布隸屬函數(shù)。
(1)式中取![]() 。仿真結(jié)果如圖2~5所示。
。仿真結(jié)果如圖2~5所示。
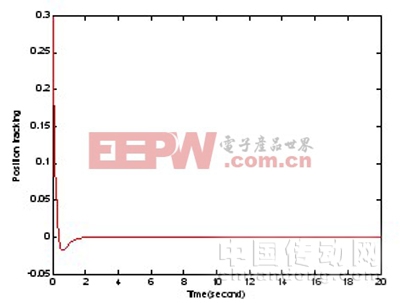
圖2 小車位置隨時間變化曲線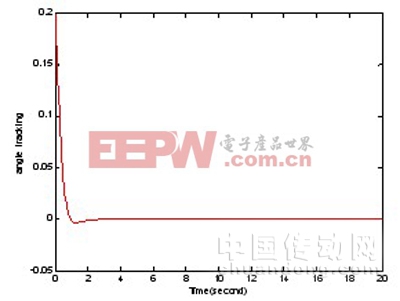
圖3 杠桿角度隨時間變化曲線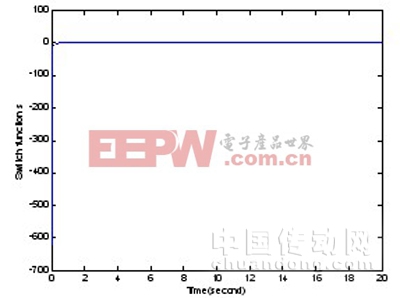
圖4 切換函數(shù)對時間變化曲線 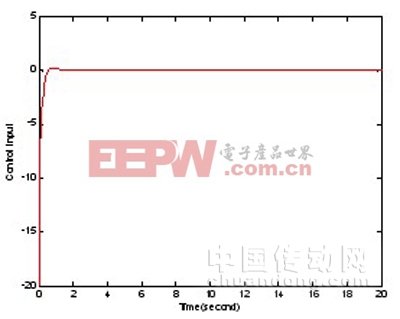
圖5 控制律隨時間變化曲線
由以上仿真結(jié)果可以看出,利用本文方案設(shè)計的控制器大大加快了系統(tǒng)的響應(yīng)速度,且能有效地減小系統(tǒng)的最大偏差,系統(tǒng)的抖振現(xiàn)象也基本可以消除。
5結(jié)論
本文介紹了蹺蹺板系統(tǒng)的工作原理,建立了蹺蹺板系統(tǒng)的數(shù)學(xué)模型。針對常規(guī)滑模控制中存在的抖振現(xiàn)象,將模糊滑模控制方法引入蹺蹺板控制系統(tǒng)中,通過仿真可以看出,將模糊滑模控制應(yīng)用于具有強耦合、非線性特性的蹺蹺板系統(tǒng)是切實可行的,而且使用滑模模糊控制算法設(shè)計出來的控制器具有很強的魯棒性。
參考文獻
[1] 蔡自興.智能控制基礎(chǔ)與應(yīng)用[M].北京:國防工業(yè)出版社,1998.
[2] Chia-Ju Wu.Quasi Time-Optimal PID Control of Multivariable Systems:A Seesaw Example[J] Journal of the Chinese Institute of Engineers,Vol.22, No.5,pp.617-625(1999)
[3] Lon-Chen Hung, Hung-Yuan Chung .Decoupled Control Using Neural Network-based Sliding-mode Controller for Nonlinear Systems[J] .Expert Systems with Applications 32 (2007) 1168C1182
[4] Jeng-HannLI, Tzuu-Hseng S. Li* and Ting-Han Ou.Design and Implementation of Fuzzy Sliding-Mode Controller for a Wedge Balancing System[J]. Journal of Intelligent and Robotic Systems 37: 285C306, 2003.
[5] Chun-Hsien Tsai, Hung-Yuan Chung. Neuro-Sliding Mode Control With Its Applications to Seesaw Systems. IEEE Transactions on Nural Networks, vol 5, No. 1, Jaunary 2004
[6] Wincon User Guide[M].522-530.2003
[7] 劉金琨. 滑模變結(jié)構(gòu)控制Matlab仿真[M].北京:清華大學(xué)出版社,2005:100-120.
[8] 劉金琨.滑模變結(jié)構(gòu)控制MATLAB仿真[M].北京,清華大學(xué)出版社,2005.







評論