基于模糊滑模控制的蹺蹺板控制系統設計

　　方程組(7)即為系統的非線性狀態方程表達式。

　　3模糊滑模控制器的設計

　　滑模變結構控制具有響應速度快、魯棒性強等優點，被廣泛應用與非線性系統控制當中，但是滑模控制容易引起系統的抖振現象，導致系統的最終不穩定。模糊滑模控制是在不確定環境下，對于復雜對象進行有效控制的一種智能控制方法。它不依賴系統的模型，而且對干擾具有完全的魯棒性，同時保持了模糊控制和滑模控制的優點。模糊滑模控制的基本設計方法是在滑模控制系統的趨近階段通過模糊邏輯調節控制作用來補償未建模動力學的影響，其目的是提高控制系統的品質、減少到達滑動面時間、降低抖振。文中利用模糊控制規則調整控制輸入量的大小，保證滑模控制到達條件得到滿足。模糊滑模控制原理如圖1所示。

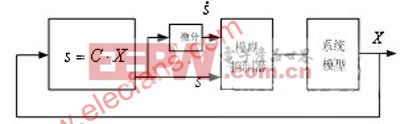
　　圖1模糊滑模控制原理圖

　　由圖可知，模糊滑模控制系統由三部分組成，即切換函數、模糊控制器、和被控對象。滑模函數的輸入為系統狀態變量，切換函數設計為s=C·X

(1)

　　模糊控制器的輸入為切換函數及其變化率，這樣可有效的減少模糊規則的數量，很好的解決高階系統多輸入中存在的規則爆炸問題。控制的變化量作為滑模控制器的輸出，可使模糊滑模控制成為無模型控制，依賴于被控對象的程度較小[7]。

　　根據模糊控制原理，定義模糊集，

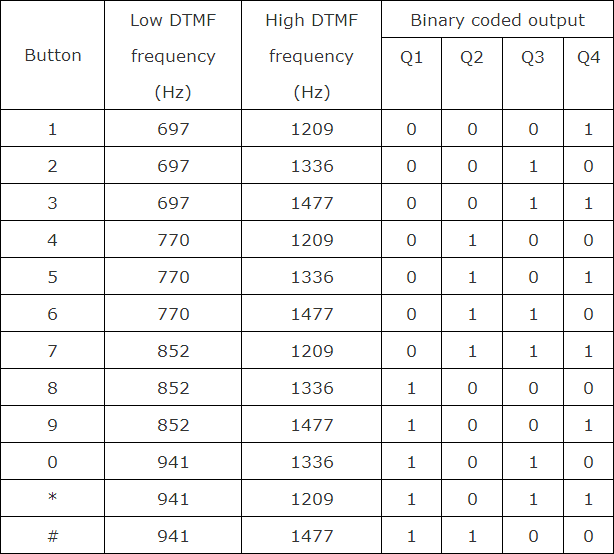
　　其中PB，PM，PS，ZO，NS，NM，NB分別表示為正大，正中，正小，零，負小，負中，負大。在滿足不等式的條件下設計，所獲得的控制表如表1所示。使用的模糊規則是

　　表1模糊控制規則表

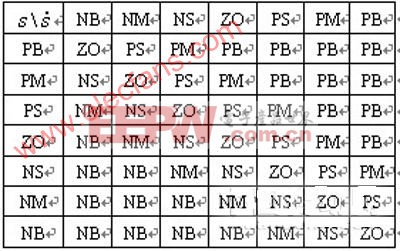
　　表中所有的控制規則是根據滿足這個達到滑模的充要條件所設計的[8]，所以設計的模糊滑模控制系統是穩定的。

　　4仿真研究

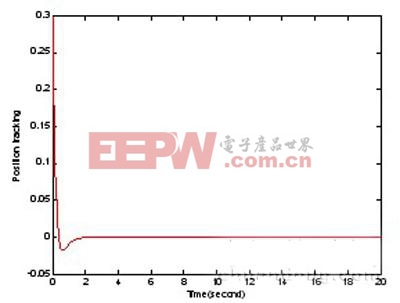
　　圖2 小車位置隨時間變化曲線