基于SVM的傳感器非線性特性校正新方法
摘 要:介紹了一種基于支持向量機(jī)的解決傳感器系統(tǒng)非線性特性問題的新方法。支持向量機(jī)是Vapnik教授提出的基于統(tǒng)計(jì)學(xué)習(xí)理論的新一代機(jī)器學(xué)習(xí)技術(shù),它有效地解決了小樣本學(xué)習(xí)問題,因此該方法對(duì)樣本數(shù)量沒有特殊的要求。實(shí)驗(yàn)證明該方法有效,同時(shí)研究表明該方法也能用于其他系統(tǒng)的非線性校正。
關(guān)鍵詞:非線性校正;神經(jīng)網(wǎng)絡(luò);支持向量機(jī);擬合方法;傳感器
0前言
現(xiàn) 代控制系統(tǒng)對(duì)傳感器的準(zhǔn)確度、穩(wěn)定性和工作條件等方面提出了很高的要求。然而,從嚴(yán)格意義上來說,目前絕大多數(shù)傳感器特性都不理想,其輸入輸出特性大多為 非線性關(guān)系。為此,人們通過一些方法來進(jìn)行非線性補(bǔ)償和修正。特別是近年來,隨著神經(jīng)網(wǎng)絡(luò)的發(fā)展,有不少學(xué)者提出了基于神經(jīng)網(wǎng)絡(luò)進(jìn)行非線性傳感特性校正的 方法。這些方法一般是用一個(gè)多層的前饋神經(jīng)網(wǎng)絡(luò)去映射傳感器特性曲線的反函數(shù)作為校正環(huán)節(jié),算法相對(duì)簡(jiǎn)單,實(shí)現(xiàn)容易。
但是通過分析神經(jīng)網(wǎng)絡(luò)的基本工作原理,筆者認(rèn)為該方法依然存在一些不足[1、6]:1)在訓(xùn)練過程中神經(jīng)網(wǎng)絡(luò)極容易陷入局部最小,而不能得到全局最小;2)神經(jīng)網(wǎng)絡(luò)過分依賴訓(xùn)練數(shù)據(jù)的質(zhì)量和數(shù)量,但大多數(shù)情況下樣本數(shù)據(jù)十分有限,由于噪聲影響,存在數(shù)據(jù)不一致情況,對(duì)神經(jīng)網(wǎng)絡(luò)的訓(xùn)練結(jié)果影響較大;3)輸入數(shù)據(jù)往往是高維的,而訓(xùn)練結(jié)果僅是輸入空間的稀疏分布,所以大量的高維數(shù)據(jù)必然會(huì)大大增加算法的訓(xùn)練時(shí)間。
支持向量機(jī)SVM[4,5](Support Vector Machine)是基于統(tǒng)計(jì)學(xué)習(xí)理論的一種新的學(xué)習(xí)方法,最早由Vapnik教授及其合作者于上世紀(jì)90年 代中期提出。由于其優(yōu)良特性,最近引起了許多研究者的興趣。支持向量機(jī)主要用于模式識(shí)別,目前在該方面成功的范例較多;與模式識(shí)別相比,支持向量機(jī)用于函 數(shù)擬合的成功應(yīng)用較少。和神經(jīng)網(wǎng)絡(luò)相比,支持向量機(jī)是基于統(tǒng)計(jì)學(xué)習(xí)理論的小樣本學(xué)習(xí)方法,采用結(jié)構(gòu)風(fēng)險(xiǎn)最小化原則,具有很好的泛化性能;而神經(jīng)網(wǎng)絡(luò)是基于 大樣本的學(xué)習(xí)方法,采用經(jīng)驗(yàn)風(fēng)險(xiǎn)最小化原則。
將支持向量機(jī)函數(shù)擬合技術(shù)應(yīng)用于傳感器非線性特性校正的研究剛起步,國內(nèi)尚無先例。如何在傳感器非線性特性校正領(lǐng)域充分發(fā)揮支持向量機(jī)函數(shù)擬合的技術(shù)優(yōu)勢(shì),解決神經(jīng)網(wǎng)絡(luò)方法中的缺陷是一個(gè)值得研究的問題。
1支持向量機(jī)擬合基本理論
1.1線性函數(shù)擬合問題
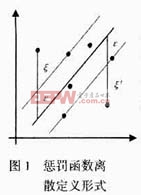
與支持向量機(jī)的研究最初是針對(duì)模式識(shí)別中的線性可分問題[5]相似,先分析線性樣本點(diǎn)的線性函數(shù)擬合問題,擬合函數(shù)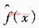 以線性函數(shù)的特性出現(xiàn),可用形式
以線性函數(shù)的特性出現(xiàn),可用形式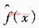 =ωTx+b表示。假設(shè)所有訓(xùn)練數(shù)據(jù){xi,yi}能在精度ε下無誤差地用線性函數(shù)擬合,即
=ωTx+b表示。假設(shè)所有訓(xùn)練數(shù)據(jù){xi,yi}能在精度ε下無誤差地用線性函數(shù)擬合,即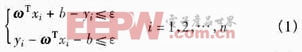









評(píng)論