電力系統混沌振蕩的自適應最優控制
加入技術交流群
3 電力系統混沌振蕩的自適應最優控制
3.1 非線性最優控制器設計
假設系統為精確建模，系統的等值阻尼系數D，發電機的機械功率Pm以及擾動功率幅值Pe已知，也就是說γ、ρ和F已知。受控的閉環系統如下式所示。
對該系統采用二次型最優控制方法，使
式中，Q、R分別對應于狀態量的權矩陣和控制量的權系數。
如果系統為精確建模，且干擾的周期性負荷的幅值已知，由控制器（6）與原系統的構成的閉環系統可知，控制器將補償系統的非線性和外部干擾，并增加了系統的阻尼，因而將抑制混沌，保證系統的漸近穩定。
3.2 自適應最優控制器設計
由于系統的不精確建模，假設系統中等值阻尼系數D、發電機機械功率Pm、擾動功率幅值Pe等一些參數不確定，即γ、ρ和F不確定，則最優控制器中γ、ρ和F這些參數由
自適應控制律來實現。同時設由最優控制律得到的最優反饋增益系數K1=K2=-1,并將△δ(t)=δ(t)
式中K3,K4,K5均為大于零的自適應控制系數。
為證明閉環系統在控制器（7）作用下能保持漸近穩定，構造如下的Lyapunov函數：
于是，閉環系統（3）在控制器（7）作用下可以保持漸近穩定，即當電力系統受擾進入混沌狀態甚至失去穩定時，其也能在控制器作用下回到初始平衡點。
4 數值仿真分析
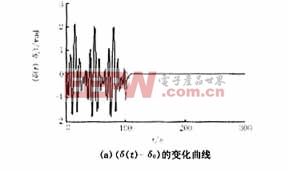
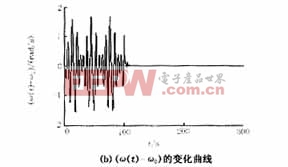
式（1）中的參數分別取為：H=100，Ps=100，D=2，Pm=20，β=1，即a=1，γ=0.02，ρ=0.2。由文獻[8]知，當Pe=25.93（F=Pe/H=0.2593），系統處于混沌狀態，如圖2（a）（b）的前100s所示；當Pe=25.94（F=0.2594)時，系統不僅處于混沌狀態，而且在t=137s時已經失去穩定，如圖3（a）、（b）的137s所示。本文引用地址：http://www.104case.com/article/162414.htm
評論