一種基于混合匹配的指紋識別方法
同時也在特征點方向匹配時設置方向誤差范圍Dw, 由于采用的是離散的8 個方向, 故范圍為Dw={Dir-1,Dir,Dir+1} , 其中當Dir=1 時,Dir-1=8;當Dir=8 時,Dir+1=1。
(6) 排序后, 將輸入點集Q 的特征點和模板點集P 中的特征點進行逐一匹配。當輸入圖像和模板圖像中超過13 對特征點滿足條件時, 則認為這兩幅指紋來自同一手指, 匹配成功; 反之, 失敗。
2DPCA 算法是一種以圖像為分析對象的特征提取算法, 因此在構造圖像協方差矩陣時, 可以直接利用圖像矩陣。2DPCA 算法以圖像的全局信息為處理對象, 在實現降維和提取特征的過程中, 賦予了圖像矩陣中每個像素相同的地位, 如果直接采用2DPCA 算法對圖像進行處理, 將不可避免地損失掉一部分類間訓練樣本所包含的判別信息。
基于以上不足,本文設計一種基于樣本類別信息的改進2DPCA 算法,該算法根據樣本類別信息的差異性,利用樣本的類內協方差矩陣作為特征向量的產生矩陣,利用類聚值向量和類間協方差矩陣來提取訓練樣本的特征。
2.1 改進的2DPCA 算法
假設訓練樣本為m×n 的圖像矩陣,總數量為P,訓練樣本的類別數為L,設第l 類的訓練樣本數量為Pl,則滿足:

對于第l 類某一幅訓練樣本X′, 其投影空間為U′,將X′投影到U′將產生一個投影矩陣Y′=X′U′ 。用投影Y′的總離散度作為準則函數J(U′)來衡量投影空間U′ 的優劣,其準則函數滿足:

其中,SU′ 是投影矩陣Y′=X′U′ 的協方差矩陣,tr (SU′ ) 為SU′的跡。對于數量為Pl的第l 類樣本圖像xi′ (i=1,2,…,Pl),可以得到樣本類的平均圖像滿足:
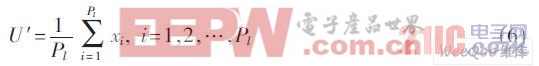
采用式(7)將該樣本類中的所有圖像去均值:

得到其協方差矩陣滿足:

在得到樣本類內的協方差矩陣G′后, 計算其特征值矩陣和特征向量矩陣。則該類樣本的特征值就是特征值矩陣的對角元素,同時得到對應的特征向量。對于每一類樣本, 取其前k 個特征值所對應的特征向量作為投影空間U′:
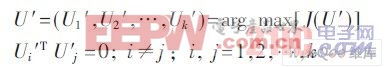
Ui′T U′j =0; i≠j ; i, j=1,2,…,k這樣, 就可以得出第l 類樣本圖像Xi′(i=1,2,…,Pl)在空間U′中的投影滿足:
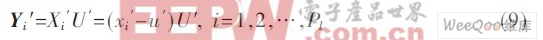
則Yi′即為該類別原始圖像xi′降維后的特征向量, 作為此類別圖像的投影向量矩陣,用來對該樣本類的圖像進行識別。同理, 將L 類共P 幅訓練樣本按樣本類別分別訓練, 可以得到L 個投影向量矩陣。
2.2 改進的2DPCA 算法的指紋匹配
指紋分類后, 將訓練樣本進行有效區域提取, 得到四類新的樣本集。然后對每一類訓練樣本進行處理, 分別得到其投影后的特征向量。










評論