基于D-S證據理論的多傳感器數據融合

摘要：D-S證據理論可以有效地處理不確定信息，是有效的數據融合方法之一，但在證據高度沖突時，其歸一化過程會產生有悖常理的結果。針對這個問題，國內外的學者提出了許多不同的改進方法，基本上可分為兩類：修改組合規則和修改融合模型。在此總結分析了相關的國內外典型文獻的改進思想，并進行系統條理的分析，為證據理論的發展和改進提供了有價值的參考。
關鍵詞：D-S證據理論；數據融合；證據沖突；傳感器

0 引言
無論在軍事上還是非軍事上，多傳感器數據融合已經成為全球研究的熱點之一。數據融合的重要研究內容之一是融合方法。最初的融合分為3個層次：像素級融合、特征級融合和決策級融合。D-S方法是決策級融合的重要方法，在數據融合領域應用極為廣泛。該方法以D-S理論，即證據理論為基礎，核心是Dempste合成規則。
Dempster-Sharer證據理論簡源于20世紀60年代Dempster在多值映射方面的工作，他將證據的信任函數與概率空間的一概率的最大、最小值相關聯構造了不確定推理模型的一般框架，此后，Sharer又在此基礎上進行了擴展，形成了能夠處理不確定不精確不完整信息的證據理論。它憑借其能夠表示不確定性未知等概念的優點在數據融合中得到廣泛重視，特別是成功應用于圖像處理、機器人導航、醫療診斷決策分析等需要處理不確定信息的領域。
證據組合規則是證據理論的核心，它將來自不同信息源的獨立證據信息組合，產生更可靠的證據信息。但是在證據高度沖突和完全沖突的情況下D-S理論的組合規則失效。在戰場環境下(特別是在敵方的電子反偵察的情況下，傳感器對目標的檢測存在漏檢、錯檢的情況，可能提供很不相同，甚至是相互矛盾的數據。這些現象造成了同一傳感器在時間上的證據沖突，D-S組合規則在此種情況下無法得出正確的結果。為此D-S組合規則的修正方法正是針對時域沖突的特點提出的。

1 研究現狀
設有一個有限假設空間，2Θ為空間中所有命題的窮舉集合，D-S理論用“識別框架(Frame of Discernment)”描述構成整個假設空間的所有命題的集合Θ，識別框架中的各元素要求互相排斥而集合中的命題稱為識別框架的原命題。
定義1 設Θ為一識別框架，2Θ為Θ的冪集，則函數m：Ω→[0，1]，在滿足下列條件：
A≠φ時，稱m為Ω上的基本概率分配；，m(A)稱為基本概率分配函數(Basic Probabil-ity Assignment，BPA)。BPA反映了證距識別框架中的命題A的支持程度。A稱為焦元，所有焦元的集合稱為核。
定義2 Θ為一識別框架，m(A)為Ω上的基本概率分配函數，滿足下列條件的函數稱為信任函數(Bilief Function)：

即A的信度函數為A中每個子集的信度值之和。
定義3 Bel為一信任函數，有一函數Pl：Ω→[0，1]，，，則Pl為A的似然函數。
定理1 m1與m2為識別框架Θ上的兩個獨立證據，Ω為的Ω冪集A、B為冪集中的元素，則這兩個證據組合后得到的組合證據為：

這就是著名的Dempster-Shafer證據組合公式利用它進行多證據組合式進行不確定推理的關鍵。
D-S組合規則的優點在于證據間的沖突較小時，證據置信度向不確定性較小的命題集中。但是，在證據嚴重沖突的情況下，組合結果往往與實際情況不相符合。而且D-S組合規則缺乏魯棒性，證據對命題具有“一票否決權”。也就是說，如果有一個證據否定了命題A，即使有絕大多數的證據證明命題A是正確的，合成結果也是否定命題A的。
假定，在區分目標A，B和C時，由2個獨立的證據源(傳感器信息源)提供的BPA分別為：


2 方法改進
2．1 對組合規則進行改進
2．1．1 Yager改進方法
1989年，Yager提出了D-S理論的失效問題，并對組合規則進行了改進。在他以后，又有許多改進方法提出，都集中于沖突信息的利用上。主要解決沖突信息在什么集合上分配，以什么方式分配兩大問題。認為，既然對于沖突的證據無法做出合理的抉擇，就應該將沖突全部付給未知項X。改進后的合成公式為：

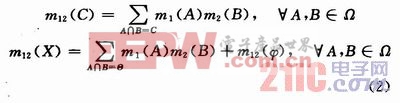
雖然該改進可以合成高度沖突的證據，但由于它對沖突證據仍然完全否定。所以當證據源多于2個時，結果并不理想。