蹺蹺板的模糊滑模控制系統設計
1引言
本文引用地址:http://www.104case.com/article/160913.htm蹺蹺板系統是一個比倒立擺系統更為復雜,更接近于實際應用的典型控制系統。它具有嚴重的非線性、強耦合、對干擾敏感、模型過于復雜等特點[2-5]。蹺蹺板系統是由一部小車、一個直流伺服電動機、兩個分別用于測量角度和位置的電位計以及蹺蹺板三角體組成。而讓蹺蹺板平衡的機制就是利用蹺蹺板系統中小車的移動來完成平衡的目的[6]。
由于蹺蹺板系統具有高度的非線性和強耦合性等特點以及變結構控制的抖振問題,本文將模糊滑模控制算法引入系統控制中以柔化控制量。使用模糊控制策略不僅可以使控制系統滑動模態的品質得到保證和改善,同時消除了滑模控制中的抖振現象。
2蹺蹺板系統的數學模型
蹺蹺板系統示意圖如圖(1)所示。
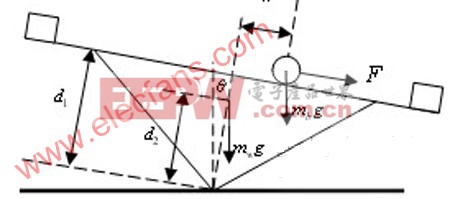
圖(1)蹺蹺板系統示意圖
圖中各參數定義如下:
杠桿的傾斜角度;X:小車的位置;d1:杠桿相對支點高度0.125m;d2:杠桿中心點相對支點高度0.058m;Iw:轉動慣量0.395kg.m2;mb:小車的質量0.57K;mw:杠桿的質量3.6K;:重力加速度9.81N/K。
定義拉格朗日算子
L=T-U(1)
其中T為系統的動能,U為系統的勢能。取狀態變量為,為構造拉格朗日方程,分別求出
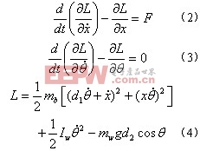
將(4)式代入(2)式和(3)式,即可得到(5)和(6)式
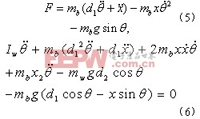
通過(5)和(6)式可分別求得和的表達式
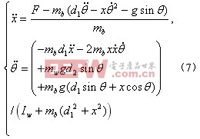









評論