基于傳感器網絡的多目標跟蹤和特征管理方法
加入技術交流群
分離的過程如圖2所示，其中K為軌跡數量，|Tk|為Tk的基數，當沒有軌跡互擾的情況下認為Tk為一個正確的軌跡。假設一條軌跡至少包含兩個觀測值，因為不能由一個單一的觀察值確定一條軌跡。于是再假設e(t-1)為時刻t-1之后目標的數量，z(t)為時刻t消失的目標的數量，c(t)=e(t-1)-z(t)為時刻t-1到t未消失的數量。設a(t)為時刻t新出現的目標，d(t)為時刻t的實際目標，g(t)=c(t)+a(t)-d(t)為未識別的目標。最后，設f(t)=n(t)-d(t)為錯誤報警數量，有：
其中P(ω|Y)是Y的相似概率。本文引用地址：http://www.104case.com/article/160284.htm
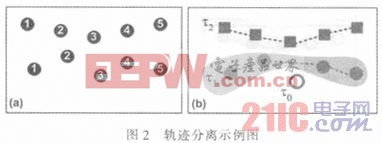
本文采用了最大后驗MAP算法解決多目標跟蹤問題。該算法對觀測目標進行分割，并根據分割對目標狀態進行估算。
3 馬爾科夫鏈蒙特卡洛數據融合
本節提出一種解決第二節中多目標跟蹤問題的算法，該算法是離散多目標跟蹤與識別算法模塊的核心。
3．1 馬爾科夫鏈蒙特卡洛模型
馬爾科夫鏈蒙特卡洛模型是已知唯一能在多項式時間復雜問題下實現估值計算的方法，同時，還是一種從位于空間Ω的分布π中提取抽樣值的普遍方法，該方法通過狀態值ω∈Ω和穩定分布值π(ω)建立的馬爾科夫鏈M來實現其算法。現在來描述該算法。在狀態ω∈Ω，假設ω’∈Ω服從分布q(ω，ω’)。而運動的感知服從感知慨率A(ω，ω’)，其中：
然而樣本保持在ω。通過計算，平衡條件得以滿足，例如，對于所有的ω：
其中，P(ω，ω’)=q(ω，ω’)A(ω，ω’)是從ω到ω’的躍遷概率。
如果M具約束性和非周期性，并且M由遍歷定理收斂至均勻分布。因此，對于一個給定的有界函數f：Ω→Rm，樣本均值
，其中ωn是M在時刻t的狀態，當Eπf(ω)收斂于N→∞。可以注意到公式(4)只需計算出π(ω’)／π(ω)的比值，而無需對π進行標準化。
3．2 馬爾科夫鏈蒙特卡洛數據關聯
MCMCDA算法是馬爾科夫鏈蒙特卡洛算法的特殊形式，其狀態空間是上文在第2．2節中提到的，并且其平穩分布服從公式(3)。對于MCMCDA的分布有5類動作組成。它們包括：1)發現／消失運動；2)分割／合并運動：3)擴展／減少運動；4)跟蹤刷新運動；5)跟蹤切換運動。
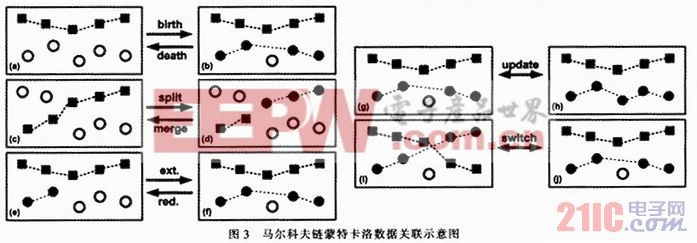
MCMCDA的運動方式如圖3中所示，每個運動的詳細描述在此省略。MCMCDA的輸入是一系列觀測值Y，樣本觀測值的個數nmc，初始狀態ωinit，以及有界函數X：Ω→Rm。對于該算法的每一步，ω是馬爾科夫鏈的當前狀態。其獲取概率A(ω，ω’)如公式(4)，輸出
接近MMSE的估計值EπX，且
接近MAP的估計值arg maxP(ω|Y)。
評論