雙電機(jī)消隙技術(shù)在某火炮隨動(dòng)系統(tǒng)中的應(yīng)用
摘要:文中以某火炮隨動(dòng)系統(tǒng)的研制為背景,為了進(jìn)一步提高系統(tǒng)精度,首先介紹了復(fù)合控制系統(tǒng)模型及分區(qū)PID算法,另外詳細(xì)論述了雙電機(jī)消隙的原理及動(dòng)力系統(tǒng)結(jié)構(gòu),并建立了仿真模型。最后,通過(guò)madab仿真表明同時(shí)運(yùn)用分區(qū)PID算法和雙電機(jī)消隙技術(shù),能夠在保證系統(tǒng)穩(wěn)定的情況下,很大程度地提高伺服系統(tǒng)跟蹤精度。
關(guān)鍵詞:復(fù)合控制;分區(qū)PID算法;雙電機(jī)消隙;仿真
眾所周知,經(jīng)典PID由于算法簡(jiǎn)單,在隨動(dòng)系統(tǒng)的控制中是十分常用的,但由于經(jīng)典PID算法的比例、積分和微分是一直不變的,這就使得它的控制效果達(dá)不到很好的效果,而采用分區(qū)PID控制,能根據(jù)實(shí)際需要,在不同區(qū)段采用相應(yīng)算法,可以在很大程度上提高系統(tǒng)的穩(wěn)定性。另外,伺服系統(tǒng)的齒輪中存在齒隙,采用雙電機(jī)消隙技術(shù)可以很好地予以克服,并使火炮跟蹤精度更高,誤差更小,魯棒性更好。
1 火炮隨動(dòng)系統(tǒng)結(jié)構(gòu)及分區(qū)PID控制算法
1.1 復(fù)合控制系統(tǒng)結(jié)構(gòu)
本系統(tǒng)使用復(fù)合控制結(jié)構(gòu),及同時(shí)使用反饋和前饋控制。在位置環(huán)分區(qū)PID控制器的基礎(chǔ)上,引入速度、加速度前饋。復(fù)合控制框圖如圖1所示。
時(shí),電機(jī)剛開(kāi)始運(yùn)行,此時(shí)輸出角和輸入角的差值最大,處在三區(qū),系統(tǒng)以最大角加速度加速再以最大角速度向平衡點(diǎn)接近,在此階段,應(yīng)該增加Kp,減小Kd,同時(shí)為了防止輸出值過(guò)大,應(yīng)當(dāng)增大Ki。
系統(tǒng)處于二區(qū)時(shí),選取PI控制,在此過(guò)程中使實(shí)際角速度向理想角速度靠攏。
在一區(qū)和零區(qū),實(shí)際位置逐漸接近預(yù)定值,為抑制超調(diào)應(yīng)減小Kp,增大Kd和Ki。
當(dāng)系統(tǒng)處于小區(qū).系統(tǒng)靜差已經(jīng)小到允許范圍內(nèi),只需要采取P控制。
2 雙電機(jī)消隙原理及數(shù)字仿真
2.1 雙電機(jī)消隙原理
2.1.1 齒隙的非線性及對(duì)系統(tǒng)穩(wěn)定性的影響
在理想情況下,伺服系統(tǒng)中的齒輪變速裝置,其輸入與輸出間的關(guān)系應(yīng)該是線性的。但實(shí)際上,由于齒輪在加工和使用中誤差的存在,以及為了補(bǔ)償由溫度和彈性形變所引起的尺寸變化,在一對(duì)相互嚙合的齒輪之間總存在一定的齒隙,圖2表示了齒輪嚙合中的間隙。
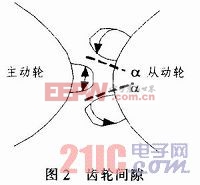
當(dāng)主動(dòng)輪運(yùn)動(dòng)方向改變時(shí),從動(dòng)輪仍保持原有位置,一直到全部齒隙2α被走完時(shí),從動(dòng)輪的位置才開(kāi)始改變。正是這個(gè)間隙的存在,使得理想的線性傳動(dòng)變成了一種非線性的傳動(dòng)過(guò)程,從而對(duì)系統(tǒng)穩(wěn)定造成影響。




評(píng)論