基于SATAII協議的CRC32并行算法的研究

摘要：在介紹CRC校驗原理和傳統CRC32串行比特算法的基礎上，由串行比特型算法推導出一種CRC32并行算法、并結合SATAⅡ協議的要求，完成了SATAⅡ主控制器設計中CRC生成與校驗模塊的設計。最后通過在ISE平臺上編寫Verilog硬件描述語言，對SATA協議中幀結構數據進行仿真，驗證該CRC32并行算法能夠滿足SATA接口實時處理的要求。
關鍵詞：CRC32；并行算法；SATA；Verilog

隨著通信和存儲技術的發展，數據傳輸速率在急劇提高。然而由于通道傳輸特性不理想及可能受到干擾或噪聲的影響，數據傳輸過程中難免會發生錯誤。如何保證可靠性是正確設計一個通信系統或數據存儲系統的關鍵問題所在。
信道編碼是提高可靠性的必要手段，實現檢錯功能的差錯控制方法很多，包括奇偶校驗、重復碼校驗、校驗和檢測、行列冗余碼校驗、恒比碼校驗、CRC校驗等。其中CRC循環冗余校驗是一種高效率的差錯控制方案，其特點是編碼和解碼的方法簡單、檢錯糾錯能力強，因而應用于許多領域尤其是串行通信中以實現差錯控制。
CRC循環校驗算法占用的系統資源少，其實現方法分為軟件實現和硬件實現。文中在研究CRC32算法的基礎上，結合SATAⅡ協議的具體要求，實現了基于FPCA的CRC32并行算法。

1 CRC校驗原理
CRC校驗算法是利用線性編碼理論，發送方根據一定的規則，生成要傳送的n位信息碼的r位校驗碼(CRC碼)，并將校驗碼附在信息碼后面，最后發送(n+r)位二進制系列。而接收方利用信息碼和校驗碼之間所遵循的同樣規則對接受到的二進制系列進行校驗，以判斷傳送中是否出錯。為了便于描述，n位信息碼用多項式k(x)表示：

由于求CRC校驗碼采用模2加減運算法則，即不帶進位和借位的按位加減，這種加減運算實際上就是邏輯上的異或運算，加法和減法在邏輯上是等價的。在模2多項式代數運算中定義的規則有：

式中R(x)即為要求的CRC校驗碼，xrk(x)+R(x)為發送端向接收端所發送的加入了CRC校驗碼的信息碼，由式(6)可知xrk(x)+R(x)能夠被生成多項式G(x)所整除。故接收端對接受到的信息以同樣的生成多項式G(x)生成其CRC校驗碼，如果為0，則表示數據傳送過程中未出錯，否則出錯，應做出相應的處理。

2 CRC32算法介紹
CRC32規范中其生成多項式G(x)如下：

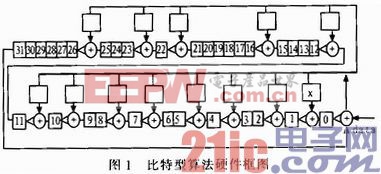
常用的CRC校驗碼生成算法包括串行比特型算法、查表型算法和并行算法。串行比特型算法主要由一個32比特移位寄存器和異或單元組成。每輸入一位串行數據，都會與移位寄存器中相應的位進行異或，異或結果保存在相應的位中，并循環移位一位，直到32位串行數據輸入完畢，再進行32次循環移位將每一位寄存器中的數據依次輸出，輸出的32位數據即為CRC32校驗值。其硬件實現框圖如圖1所示。