基于FPGA的數字下變頻的研究與實現

l 常用數字下變頻結構
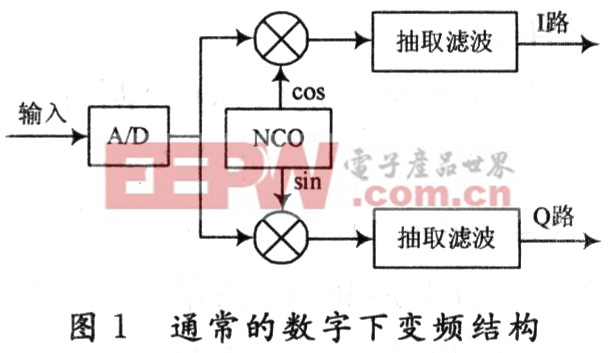
通常的數字下變頻結構如圖1所示。可以把數字下變頻分為兩個基本的模塊，數控振蕩器：NCO(Nu-merical Control Oscillator)混頻模塊和抽取濾波模塊。其中NCO模塊產生正余弦波樣本值，然后分別與輸入數據相乘，完成混頻。
抽取濾波模塊常用的結構是積分梳狀抽取濾波器(CIC)級聯后再與多級半帶濾波器(HBF)的級聯。如果信號帶寬比較寬，抽取倍數不是很大，可以采用FIR濾波器。當輸入信號采樣速率很大的時候，則可以采用多相濾波的下變頻方案，把運算環節安排在抽取之后，這種結構大大降低了對數據處理速度的要求。

2 信號下變頻方案的設計
設信號的中頻頻率為典型值70 MHz，帶寬為lO MHz，則基帶帶寬B為5 MHz。由Nyquist采樣定理，對該信號的采樣頻率不能低于2B即10 MHz，實際應用中一般大于2．5B即12．5 MHz。現階段商用數字下變頻芯片都是基于CIC和HBF級聯方式設計的，當采樣率大抽取倍數小時，芯片處理帶寬比較窄，濾波器組的濾波性能也不理想。同時DSP芯片數據處理速度達不到要求，所以采用FPGA實現該數字下變頻系統。
2．1 采樣頻率fs的確定
由于過采樣的頻率要求達到150 MHz以上，速率比較高，不易實現，所以設計方案采用帶通采樣。由Shannon帶通采樣定理，設f(t)為一帶通信號，其通稀為(fL，fH)，在實信號采樣情況下，其采樣頻率fs應滿足以下條件，才能從其采樣信號重構恢復f(t)：

式中：N為滿足后式的某一正整數。由后式可以算出1≤N≤6，當N取不同值時，各采樣率取值范圍如表1所示。

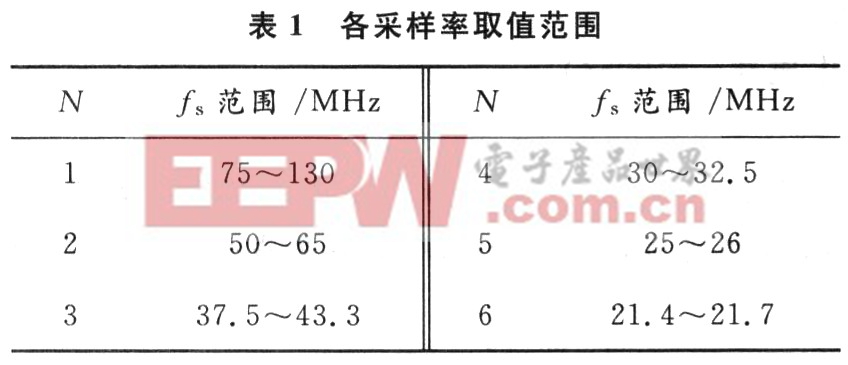
采樣率高，ADC前的抗混疊濾波器比較容易實現，同時ADC信噪比(SNR)公式如下：
SNR=[6．02b+1．76+101g(fs／2B)]dB
式中：b是ADC的采樣位數。可見采樣率越高，ADC的SNR也越高。所以，應提高采樣率，但是同時也應考慮到后級運算速度情況。
2．2 NCO的設計
主要的下變頻方法有以下四種：
(1)查表法產生正余弦波樣本值，然后混頻。
(2)IIR振蕩器產生數字化正余弦函數，然后混頻。
(3)采用流水線技術的坐標旋轉數字式計算機(CORDIC)算法。
(4)重采樣。
實際中用得最多的還是(1)，(3)兩種方法。
方法(1)產生以下正余弦波樣本值：
s(n)=cos[2π(fc／fs)n]， n=O，1，2，…
式中：fc為NCO的本振頻率，滿足fc=70-fs，這些樣本值與信號采樣值相乘完成混頻。
采用查表法要實現比較高的精度需要大量的FP-GA ROM資源，而方法(3)則不需要耗費這么大的資源，雖然采用流水線技術會使輸出產生迭代次數個時鐘周期的延遲，但是可以省略兩個乘法器，是比較好的實現方式。
進一步研究采樣率，令fs=Mfc，由s(n)的表達式知，如果M為整數時，明顯樣本值可以由龐大的查找表數據簡化為M個數據，將fs=Mfc代入fc=70-fs中，可得：

結合表1和上式，綜合考慮各種情況，取N=2，M=4，fs=56 MHz，則s(n)=cos(πn/2)，n=O，1，2，…。可以看出正余弦波樣本值只為1，-1，0，混頻時只是對輸人數據進行保持不變，取負和置0操作，省略了兩個乘法器，最大程度地節約了資源，同時也避免了正余弦值位數截斷帶來的非正交誤差。
2．3 抽取濾波器的設計
由上面的討論，采樣率確定為56 MHz，精度為12 b。對輸入數據進行四倍的抽取，所得到的數據速率為14 MHz，大于12．5 MHz，滿足要求。
CIC濾波器適合窄帶高抽取率的情況，用在此處并不合適，故采用FIR濾波器作為抽取抗混疊濾波器，并且把四倍抽取分為兩級兩倍抽取，兩級抽取均使用半帶濾波器。
選用System View的Linear Sys Filters進行濾波器設計，用等紋波法使設計誤差在整個頻帶內均勻分布。第一級半帶濾波器參數如下：采樣率fs=56 MHz，濾波器通帶截止頻率為5 MHz，阻帶起始頻率為(56／2)-5=23 MHz，過渡帶帶寬為23-5=18 MHz，阻帶衰減為-60 dB，通帶紋波系數為0．01 dB 。由于濾波器的阻帶起始頻率較大，過渡帶相應較寬，設計出的半帶濾波器階數只有ll階，系數進行12 b量化后值如下：

[36，0，-230，0，1 217，2 047，1 217，0，-230，0，36]
同理，第二級半帶濾波器的階數為23階，系數量化值為：
[-10，0，33，O，-80，0，172，0，-376，O，1 285，2 047，1 285，0，-376，0，172，0，-80，O，33，0，-10]

3 方案的FPGA實現
由以上NCO的設計可知，混頻部分非常容易實現，關鍵部分在于濾波器的實現。
設計工具產生的半帶濾波器具有對稱結構，可只利用其中一半的系數。考慮到濾波器數據輸入速率比較高和FPGA資源的節約，采用全并行的分布式算法(DA)濾波器，每個時鐘周期能完成一次濾波運算。