FIR數(shù)字濾波器的FPGA實(shí)現(xiàn)研究
根據(jù)單位脈沖響應(yīng)的不同,數(shù)字濾波器主要分為有限脈沖響應(yīng)(FIR)和無(wú)限脈沖響應(yīng)(IIR)2大類(lèi)。在同樣的設(shè)計(jì)要求下,IIR方式計(jì)算工作量較小。但難以得到線(xiàn)性相位響應(yīng),且系統(tǒng)不易穩(wěn)定;FIR方式的計(jì)算工作量稍大,但在設(shè)計(jì)任意幅頻特性時(shí),能保證嚴(yán)格的線(xiàn)性相位特性;由于其實(shí)現(xiàn)結(jié)構(gòu)主要是非遞歸的,F(xiàn)lR濾波器可以穩(wěn)定工作。FIR數(shù)字濾波器是數(shù)字多普勒接收機(jī)的重要組成部分,因此,研究FIR數(shù)字濾波器的實(shí)現(xiàn)技術(shù)具有重要意義。隨著FPGA技術(shù)的不斷發(fā)展,F(xiàn)PGA逐漸成為信號(hào)處理的主流器件。而在FPGA中,數(shù)字濾波器不同的實(shí)現(xiàn)方法所消耗的FPGA資源是不同的,且對(duì)濾波器的性能影響也有較大差異。
1 FIR濾波器的原理及結(jié)構(gòu)
FIR濾波器存在N個(gè)抽頭的h(n),N稱(chēng)為濾波器的階數(shù),其數(shù)學(xué)表達(dá)式為:
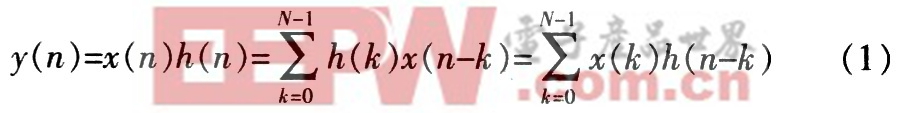
式中,x(k)為第k時(shí)刻的采樣值,y(n)為濾波器輸出。h(k)為FIR濾波器的第k級(jí)抽頭系數(shù)。
通過(guò)對(duì)h(k)進(jìn)行Z變換得到FIR的傳遞函數(shù)H(Z),其在Z域內(nèi)的形式如下:
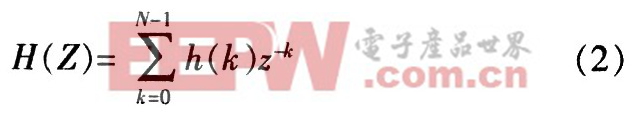
因此,根據(jù)傳遞函數(shù)H(Z)和FIR濾波器系數(shù)的對(duì)稱(chēng)性,可得FIR濾波器的一般實(shí)現(xiàn)結(jié)構(gòu),如圖1所示。
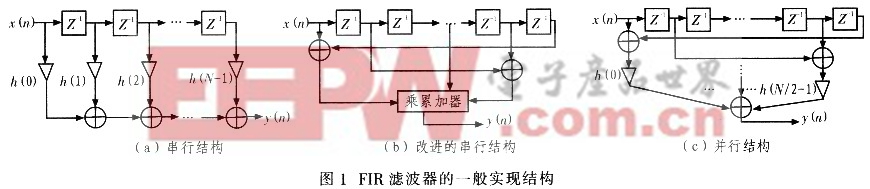
從串行結(jié)構(gòu)中可以看出,F(xiàn)IR濾波過(guò)程就是一個(gè)信號(hào)逐級(jí)延遲的過(guò)程,將各級(jí)延遲輸出加權(quán)累加,得到濾波輸出,其中最主要的運(yùn)算是乘累加運(yùn)算。FIR每完成一次濾波過(guò)程需要進(jìn)行N次乘法和(N-1)次加法運(yùn)算,N為濾波器的階數(shù)。所以,濾波器的運(yùn)算量完全取決于N的大小,當(dāng)N很大時(shí),延遲將非常長(zhǎng),無(wú)法實(shí)現(xiàn)高速信號(hào)處理。
根據(jù)FIR數(shù)字濾波器的對(duì)稱(chēng)特性,可以先進(jìn)行加法運(yùn)算,然后對(duì)加法運(yùn)算的結(jié)果進(jìn)行串行乘累加運(yùn)算,從而得到改進(jìn)的串行結(jié)構(gòu)。與串行結(jié)構(gòu)相比,改進(jìn)的濾波器完成一次濾波的時(shí)鐘周期減半,乘累加次數(shù)減半,提高了處理速度,但同時(shí)要消耗更多的硬件資源。圖1(b)為Ⅳ位偶數(shù)時(shí)改進(jìn)的串行結(jié)構(gòu)。與串行結(jié)構(gòu)相似,濾波器的運(yùn)算量完全取決于N的大小,當(dāng)N很大時(shí),延遲將非常長(zhǎng),無(wú)法實(shí)現(xiàn)高速信號(hào)處理。
將串行結(jié)構(gòu)展開(kāi),根據(jù)濾波器的信號(hào)流圖用多個(gè)乘法器和加法器并行實(shí)現(xiàn),得到FIR濾波器的并行實(shí)現(xiàn)結(jié)構(gòu),如圖1(c)所示。并行濾波器的濾波速度快,一個(gè)時(shí)鐘周期內(nèi)完成一次濾波,但消耗大量的FPGA資源,如乘累加器,且器件的延遲較大,工作頻率不宜太高。
FPGA具有規(guī)整的內(nèi)部邏輯陣列和豐富的連線(xiàn)資源,特別適合用于數(shù)字信號(hào)處理。但以前FPGA一般用于系統(tǒng)邏輯或時(shí)序控制,很少應(yīng)用在信號(hào)處理方面。其原因主要是FPGA中缺乏實(shí)現(xiàn)乘法運(yùn)算的有效結(jié)構(gòu)。隨著FPGA技術(shù)的不斷發(fā)展,查找表(LUT)技術(shù)的應(yīng)用有效地解決了這個(gè)問(wèn)題,使FPGA在數(shù)字信號(hào)處理方面得到了廣泛應(yīng)用。
2 基于分布式算法的FIR濾波器的實(shí)現(xiàn)
2.1 分布式算法原理
上世紀(jì)70年代Croisie提出了分布式算法DA(Distributed Arithmetic),但由于其特別適合用FPGA實(shí)現(xiàn),所以直到Xilinx公司在FPGA中使用查找表(LUT)后,DA才被廣泛應(yīng)用在FPGA求乘積和中。
FIR的濾波輸出y可以表示為輸入x和系數(shù)h的內(nèi)積:

由上述推導(dǎo)可知,分布式算法是一種以實(shí)現(xiàn)乘加運(yùn)算為目的的運(yùn)算方法。它與傳統(tǒng)實(shí)現(xiàn)乘加運(yùn)算的先后順序不同。分布式算法在完成乘加功能時(shí),是通過(guò)將各輸入數(shù)據(jù)每一對(duì)應(yīng)位產(chǎn)生的部分積預(yù)先進(jìn)行相加形成相應(yīng)部分積,然后在對(duì)各部分積預(yù)先進(jìn)行累加形成最終結(jié)果;而傳統(tǒng)算法是等到所有乘積產(chǎn)生之后再進(jìn)行相加來(lái)完成乘加運(yùn)算。
2.2 分布式FIR的實(shí)現(xiàn)結(jié)構(gòu)
圖2為分布式FIR濾波器的直接實(shí)現(xiàn)結(jié)構(gòu)。對(duì)于小位寬的數(shù)據(jù),DA算法不僅速度快,而且所占用的芯片資源少。
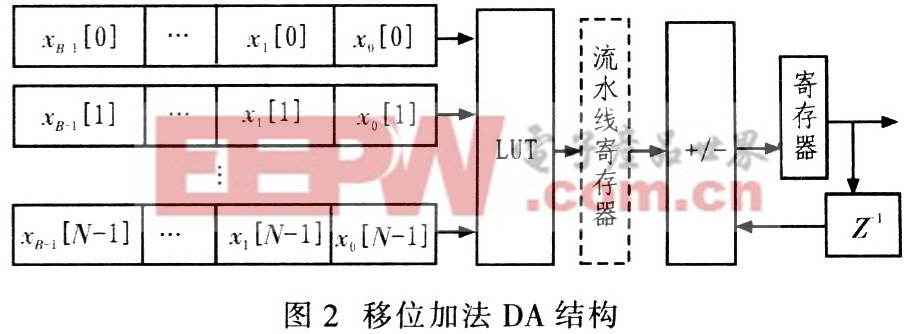
2.3 性能優(yōu)化方法
1)流水線(xiàn)結(jié)構(gòu)法 在濾波器中間增加適當(dāng)?shù)募拇嫫鳎瑯?gòu)成流水線(xiàn)結(jié)構(gòu)。在并行結(jié)構(gòu)實(shí)現(xiàn)中添加流水線(xiàn)結(jié)構(gòu),可以提高濾波器速度,使其工作在更高的工作頻率。對(duì)于速度固定的數(shù)據(jù),可以通過(guò)多次復(fù)用乘累加器來(lái)節(jié)省資源。
2)查找表分隔法 在用LUT實(shí)現(xiàn)分布式算法時(shí),由于LUT的規(guī)模隨著N的增加呈現(xiàn)指數(shù)增長(zhǎng),如果濾波器系數(shù)N過(guò)大,則查找表的規(guī)模十分龐大。為了減小規(guī)模,可以利用部分表計(jì)算。由于FIR濾波器是線(xiàn)性濾波器,因此低階濾波器輸出可以相加,由此定義一個(gè)高階濾波器的輸出。例如,把16輸入的查找表分割成4個(gè)并行的查找表。
查找表的分隔技術(shù)和流水線(xiàn)技術(shù)可以大大減小設(shè)計(jì)規(guī)模,同時(shí)并不會(huì)降低濾波速度。使用DA算法實(shí)現(xiàn)的FlR濾波器與傳統(tǒng)的算法相比,DA算法可以極大地減少硬件電路規(guī)模,很容易實(shí)現(xiàn)流水線(xiàn)處理,提高電路的執(zhí)行速度。











評(píng)論