系統的數學模型―微分方程與傳輸算子
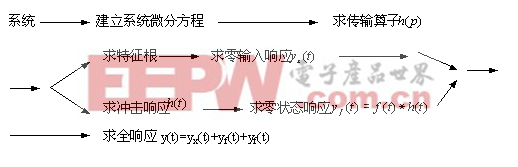
不涉及任何數學變換,而直接在時間變量域內對系統進行分析,稱為系統的時域分析。其方法有兩種:時域經典法與時域卷積法。 本文引用地址:http://www.104case.com/article/155510.htm時域經典法就是直接求解系統微分方程的方法。這種方法的優點是直觀,物理概念清楚,缺點是求解過程冗繁,應用上也有局限性。所以在20世紀50年代以前,人們普遍喜歡采用變換域分析方法(例如拉普拉斯變換法),而較少采用時域經典法。20世紀50年代以后,由于δ(t)函數及計算機的普遍應用,時域卷積法得到了迅速發展,且不斷成熟和完善,已成為系統分析的重要方法之一。時域分析法是各種變換域分析法的基礎。 在本章中,首先建立系統的數學模型——微分方程,然后用經典法求系統的零輸入響應,用時域卷積法求系統的零狀態響應,再把零輸入響應與零狀態響應相加,即得系統的全響應。其思路與程序是: |
|
其次,將介紹:系統相當于一個微分方程;系統相當于一個傳輸算子H(p);系統相當于一個信號——沖激響應h(t)。對系統進行分析,就是研究激勵信號f(t)與沖激響應信號h(t)之間的關系,這種關系就是卷積積分。 |
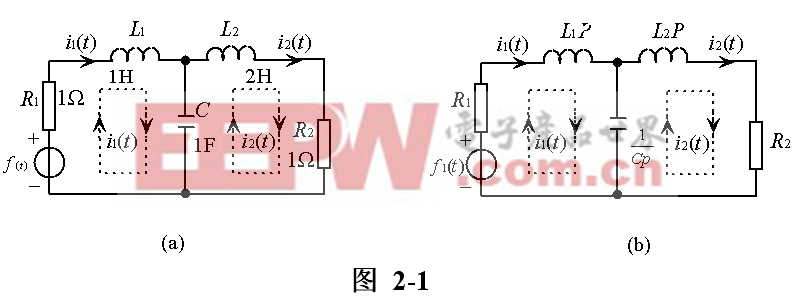
研究系統,首先要建立系統的數學模型——微分方程。建立電路系統微分方程的依據是電路的兩種約束:拓撲約束(KCL,KVL)與元件約束(元件的時域伏安關系)。為了使讀者容易理解和接受,我們采取從特殊到一般的方法來研究。 圖2-1(a)所示為一含有三個獨立動態元件的雙網孔電路,其中 |
| |||
上兩式為含有兩個待求變量 為了得到只含有一個變量的微分方程, 須引用微分算子 | |||
| |||
在引入了微分算子 | |||
| |||
即 | |||
| (2-1) | ||
根據式(2-1)可畫出算子形式的電路模型,如圖2-1(b)所示。將圖2-1(a)與(b)對照, 可很容易地根據圖2-1(a)畫出圖2-1(b),即將L改寫成Lp,將C改寫成 其余一切均不變。當畫出了算子電路模型后,即可很容易地根據圖2-1(b)算子電路模型列寫出式(2-1)。 | |||
| |||
給式(2-1)等號兩端同時左乘以p,即得聯立的微分方程,即 | |||
|
| ||
將已知數據代入上式,得 | |||
|
| (2-2) | |
用行列式法從式(2-2)中可求得響應i1(t)為 | |||
| |||
注意,在上式的演算過程中,消去了分子與分母中的公因子p。這是因為所研究的電路是三階的, 因而電路的微分方程也應是三階的。但應注意,并不是在任何情況下分子與分母中的公因子都可消去。 有的情況可以消去,有的情況則不能消去,視具體情況而定。故有 | |||
| |||
即 | |||
| |||
即 | |||
| |||
上式即為待求變量為i1(t)的三階常系數線性非齊次常微分方程。 方程等號左端為響應i1(t)及其各階導數的線性組合, 等號右端為激勵f(t)及其各階導數的線性組合。 | |||
利用同樣的方法可求得i2(t)為 | |||
| |||
即 | |||
| |||
即 | |||
| |||
即 | |||
| |||
上式即為描述響應i2(t)與激勵f(t)關系的微分方程。 | |||
推廣之,對于n階系統,若設y(t)為響應變量, f(t)為激勵,如圖2-2所示,則系統微分方程的一般形式為 | |||
| (2-3) | ||
| |||
用微分算子 | |||
| |||
或寫成 | |||
| |||
又可寫成 | |||
| |||
式中 |
| ||
稱為系統或微分方程式(2-3)的特征多項式; | |||
| |||
| (2-4) | ||
H(p)稱為響應y(t)對激勵f(t)的傳輸算子或轉移算子,它為p的兩個實系數有理多項式之比, 其分母即為微分方程的特征多項式D(p)。H(p)描述了系統本身的特性,與系統的激勵和響應無關。 | |||
這里指出一點:字母p在本質上是一個微分算子,但從數學形式的角度,以后可以人為地把它看成是 一個變量(一般是復數)。這樣,傳輸算子H(p)就是p的兩個實系數有理多項式之比。 | |||
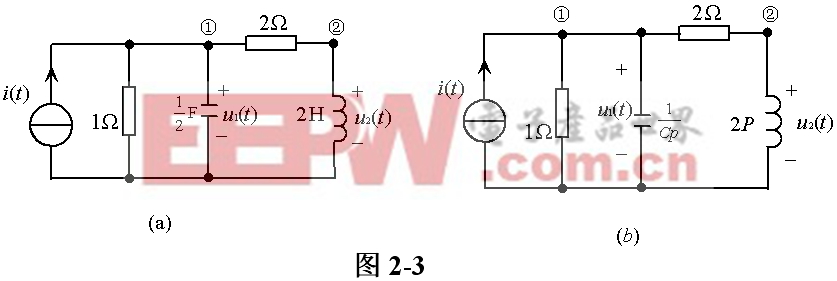
例2-1 圖2-3(a)所示電路。求響應u1(t),u2(t)對激勵 | |||
| |||
解 其算子形式的電路如圖2-3(b)所示。對節點①,②列算子形式的KCL方程為 | |||
| |||
代入數據得 | |||
| |||
對上式各項同時左乘以p,并整理得 | |||
| |||
用行列式法聯解得 | |||
| |||
| |||
故得u1(t)對i(t),u2(t)對i(t)的傳輸算子分別為 | |||
| |||
| |||
進而得u1(t),u2(t)分別對i(t)的微分方程為 | |||
| |||
| |||
即 | |||
| |||
| |||
可見,對不同的響應u1(t),u2(t),其特征多項式 這就是系統特征多項式的不變性與相同性。 | |||


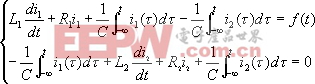
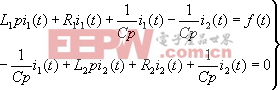
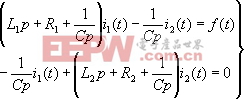
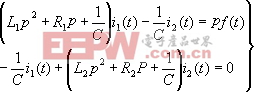
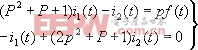
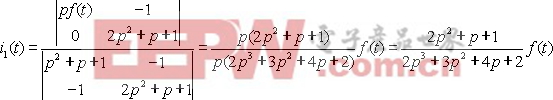


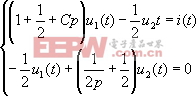
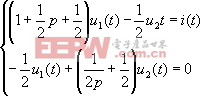
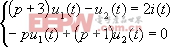


評論