系統微分方程的解―系統的全響應

一、 線性系統微分方程線性的證明

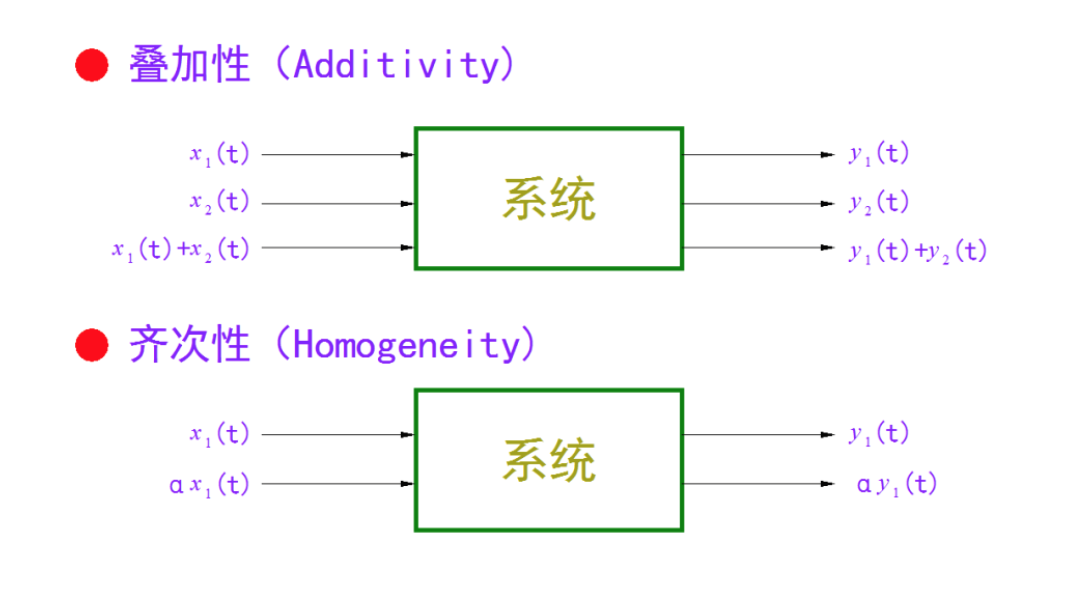
線性系統必須同時滿足齊次性與疊加性。所以，要證明線性系統的微分方程是否是線性的，就必須證明它是否同時滿足齊次性與疊加性。

線性系統微分方程的一般形式是

(2-5)

設該方程對輸入f1(t)的解是y1(t)，則有

(2-6)

設該方程對輸入f2(t)的解是y2(t)，則有

(2-7)

給式(2-6)等號兩端同乘以任意常數A1，給式(2-7)等號兩端同乘以任意常數A2，則有

將此兩式相加即有

這就是說，若 f1(t) y1(t), f2(t) y2(t) 則 A1f1(t)+A2f2(t) A1y1(t)+A2y2(t)，即式(2-5)所描述的系統是線性的。

二、 系統微分方程的解——系統的全響應

求系統微分方程的解，實際上就是求系統的全響應y(t)。系統微分方程的解就是系統的全響應y(t)。線性系統的全響應y(t)，可分解為零輸入響應yx(t)與零狀態響應yf(t)的疊加，即 。下面證明此結論。

在圖2-2中，若激勵f(t)=0，但系統的初始條件不等于零，此時系統的響應即為零輸入響應yx(t)，如圖2-4(a)所示。根據式(2-5)可寫出此時系統的微分方程為:

(2-8)

在圖2-2中，若激勵 ，但系統的初始條件等于零(即為零狀態系統)，此時系統的響應即為零狀態響應yf(t)，如圖2-4(b)所示。根據式(2-5)可寫出此時系統的微分方程為

(2-9)

將式(2-8)與式(2-9)相加得

即

式中

可見 確是系統微分方程(2-5)的解。這個結論提供了求系統全響應y(t)的途徑和方法，即先分別求出零輸入響應yx(t)與零狀態響應yf(t)，然后再將yx(t)與yf(t)疊加，即得系統的全響應y(t)，即 。這種方法稱為零輸入零狀態法。