改進遺傳算法的支持向量機特征選擇解決方案介紹

交叉操作的作用是通過交換兩個染色體之間的若干位從而生成含有部分原始優良基因的新個體。由式(3)可知互敏感度信息量可作為不同特征之間含有相似分類信息的一種度量，所以可以將互敏感度信息量代入式(4)計算出染色體在第位發生交叉的幾率b(i)，在式(4)中i和j分別代表特征i和特征j，是染色體的長度。b(i)是特征i相對于其他所有特征在互敏感度信息量上的歸一量，反映了特征與其余特征在相似信息量上的總和。由此對應到染色體上，b(i)就可以認為是染色體的第i位與整個染色體在基因信息上的相關性，b(i)越小則說明相關性越大，第i位與整個染色體所含的基因信息越接近，此位為分裂點的幾率越小。由于b(i)是歸一化量，故可采用輪盤算法來選擇一個交叉點。

變異操作是引入新物種的重要手段，可以有效地增加種群個體的多樣性。本文中的變異率Pm采用相鄰兩代之間的最優適應度增幅比作為自變量進行自適應調節，如式(5)所示。當適應度增幅比正向增大時，較小的增幅比可以使變異率維持在中等水平，并且變異率隨著增幅比的增大而緩慢降低，這樣既能夠擁有一定數量的新個體也可以抑制過多不良染色體的產生，保證優秀染色體的進化足夠穩定;而當適應度增幅比反向增大時，由較小增幅比則可以獲得較高的變異率，并且變異率也伴隨增幅比同比緩慢升高，確保有足夠的染色體發生變異，穩定地加快進化速度。

　式中dis指新生種群的最優適應度相對于原種群的最優適應度的增幅比，j與k均是區間(0，1)上的調節系數。文中的j與k分別取0.65和0.055。

　　獨立敏感度信息量在一定程度上體現了單個特征所含有的分類信息量，如果獨立敏感度信息量小，則說明該特征所含信息大部分對分類沒有幫助，即該基因位發生突變后對整個染色體的優異性影響不大，突變的概率也就相應減小。因此將獨立敏感度信息量歸一化后所得到的q(i)作為特征i被選為變異點的概率。變異點的具體選擇方法為：針對一個染色體按照染色體的位數進行循環遍歷，在該循環中由變異率Pm判定是否產生變異位。若需要產生變異位，則依據q(i)按照輪盤算法進行選擇。

　　模擬退火選群

　　在每一輪進化完成后都需要決定進入下一輪進化的種群。如果過多地將較優種群作為父代，就會使算法過早收斂或搜索緩慢。文獻[7]中指出模擬退火算法能夠以一定的概率接受劣解從而跳出局部極值區域并最終趨于全局最優解，因此可以將上文提到的最優適應度增幅比作為能量函數，運用模擬退火的Meteopolis準則來選擇待進化的種群。為了使每個種群得到充分地進化，預防最優解的丟失，這里采用設置退火步長的策略來實現模擬退火選群。該策略具體為：使退火步長對同一種群作為父代的次數進行計數，一旦產生更優種群則退火步長就置零并重新計數。若退火步長累計超過一定的閾值時，就進入模擬退火選群階段。退火步長累計到一定數量意味著原有種群的進化已經停滯，需要用模擬退火算法擺脫這種停滯狀態。如果增幅比大于零，則說明新生種群優于原有種群，這時完全接受新種群進入下一輪進化;否則新生種群劣于原有種群，并以一定的概率p接受較劣的新生種群[8]進入下一輪進化。接受概率p由式(6)和式(7)共同決定，其中dis為增幅比，T(s)指溫度參數，T0和s分別是初始溫度和迭代次數。

　　以上兩式的參數要滿足進化對接受概率的要求。即增幅比負增長越大，接受概率降低越迅速，但接受概率隨迭代次數的增加應緩慢下降。這樣做能夠保證在有限的迭代次數內有一個適應度較優的新生種群進入下一輪進化，以達到減少計算量和優選待進化種群的目的。在本文中T0=0.2，A=0.9，m=0.5。

　　實例的驗證與分析

　　UCI數據庫常用來比較各種方法的分類效果，因此可以用其驗證本算法對支持向量機作用后的分類效果[9][10]。文獻[11]采用了UCI數據庫中的German、Ionosphere和Sonar三種數據作為實驗對象，為了便于與文獻[11]中所用的幾種方法進行對比，本文也采用這三種數據進行實驗，并按照文獻中所述的比例將各類數據分成相應的訓練樣本和測試樣本。

　　在種群規模為30，交叉率為0.8，起始變異率為0.1的條件下使用支持向量機作為分類器(懲罰參數為13.7，徑向基核函數參數為10.6)對所選數據進行分類，表1中顯示了本文算法與文獻[11]中幾種算法在分類效果上的對比，表2給出了三種數據的最終選擇結果。表1中共出現了四種方法：方法1：使用本文算法;方法2：使用NGA/PCA方法;方法3：使用PCA方法;方法4：使用簡單遺傳算法。

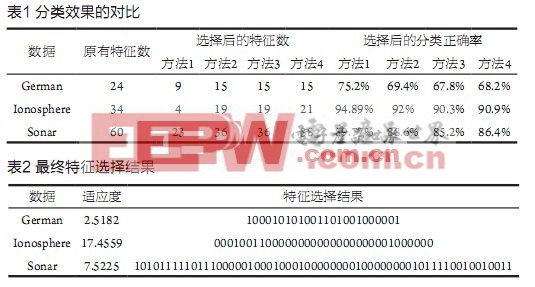
　　由于本文算法旨在用最少的特征個數最大化分類正確率，因此從表1中可以看出本文算法在特征選擇個數和分類正確率上均比其他三種方法更具優勢。由于NGA/PCA算法是針對簡單遺傳算法和主成分分析法的不足而做的改進，其性能優于簡單遺傳算法和主成分分析法，所以本文算法的分類效果優于NGA/PCA算法這一事實更能說明該算法可以較好地解決支持向量機的特征選擇問題。

　　結語

　　通過與其他方法的比較，本文算法的分類效果得到了充分的驗證，也說明了該算法具有極好的泛化能力以及在敏感度信息量地指導下遺傳操作的有效性。

　　適應度函數的設計至關重要，它直接影響到最終結果的優劣以及算法的收斂性，所以在適應度函數的設計應考慮所解決問題的側重點。

　　分類正確率的高低不僅取決于合理的特征選擇，而且與支持向量機的參數優化有關。只有在合理的特征選擇和參數優化的前提下，支持向量機分類器才能發揮出最佳的分類效果。

　　由于算法能夠較好地解決支持向量機的特征選擇問題，因此已被應用在基于支持向量機的數字電路板故障診斷當中，并取得了良好的效果。