基于具有量子行為的粒子群優(yōu)化算法慣性權(quán)重研究及應(yīng)用
Step 5 用個(gè)體粒子的速度產(chǎn)生用以選擇該粒子位置的更新方程的數(shù)據(jù);
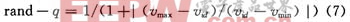 |
Step 6 由Step 5產(chǎn)生的數(shù)據(jù)選擇更新粒子位置的方程;
|
Step 7 若未達(dá)到終止條件(足夠小的適應(yīng)值或預(yù)設(shè)的最大迭代次數(shù)),則返回Step 3。
更新粒子速度時(shí)需要注意:如果粒子的速度超出預(yù)設(shè)的范圍,則采取使粒子反向運(yùn)動的策略,從而保證算法有效進(jìn)行。
1.3 算法的結(jié)果及數(shù)據(jù)分析
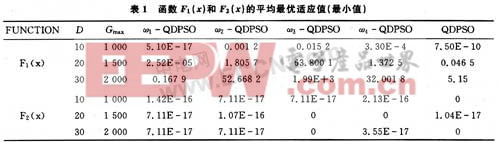
目標(biāo)函數(shù)為F1(x)和F2(x),基本參數(shù)是:c1=c2=2.05,g=0.968 5,每種算法都在同一臺計(jì)算機(jī),同一環(huán)境下用Matlab 7.1.0軟件運(yùn)行。結(jié)果如表1所示。
|
表1的數(shù)值是對每個(gè)函數(shù)在粒子數(shù)為20個(gè)的條件下,測試50次,然后取平均得到的結(jié)果。從表中可以看出,對于函數(shù)F1(x),比較結(jié)果可以明顯得知:在隨粒子群維數(shù)增加的情況下,ω1-QDPSO是比QDPSO得到更好的解,其他幾種改進(jìn)方案的解都比較差;函數(shù)F2(x)在隨粒子群維數(shù)增加的情況下,4種改進(jìn)方案和QDPSO都能得出比較好的解。
通過實(shí)驗(yàn),可以看出:對于單峰函數(shù)F1(x),ω的遞減不能太小,從方案ω1-QDPSO和ω2-QDPSO的結(jié)果就可以比較出來,而方案ω3-QDPSO和ω4-QDPSO的結(jié)果不好,可能是因?yàn)樗鼈兯阉鞯膮^(qū)域太小,從而陷入局部最優(yōu)解。
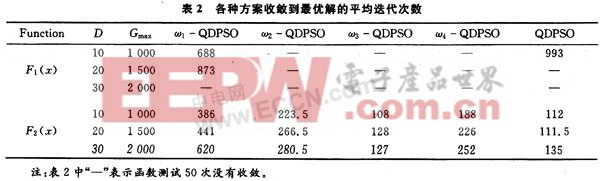
對于多峰函數(shù)F2(x),ω的變化對測試函數(shù)的解的精確度沒有太大影響,說明了改進(jìn)方案在此方面沒有明顯提高。接下來,我們還對算法的收斂速度進(jìn)行了比較。結(jié)果如表2所示。
|
表2是對函數(shù)測試50次后取得平均值的結(jié)果。可見對于函數(shù)F1(x),ω1-QDPSO和QDPSO都在10維的情況下收斂,而20維時(shí)只有ω1-QDPSO收斂,其他函數(shù)都沒有收斂,導(dǎo)致這種結(jié)果的原因有2種:


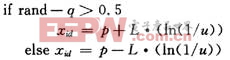





評論