基于DSP 的特定消諧脈寬調制波的實現

　　在特定消諧技術中， 首先是根據人為設計的逆變器輸出波形的特點及擬消除諧波的次數和個數來建立輸出波形的數學模型，然后由數學模型求解開關角以得到所希望的輸出波形，從而達到使逆變器的輸出波形中不含擬消除次數及個數諧波的目的。

　　為了說明特定諧波消除的原理， 這里以最常見、應用最廣泛的單相電壓型逆變器為研究對象，建立特定消諧技術的數學模型。

　　圖1 所示的輸出電壓波形的付立葉級數可以表示為：

　　實際應用中， 我們構造的單相輸出電壓波形f (wt) 既是奇函數，又是奇諧函數，即f (wt) 在[0，p ]區間以p / 2 點為軸對稱，在[0， 2p ]區間以p 點為點對稱， 因此：

　　將式(4)、式(5)代入式(2)、式(3)，可以求出付立葉級數的余弦分量、直流分量、偶次正弦分量和奇次正弦分量， 其中余弦分量、自流分量、偶次正弦分量為零， 即：

　　而奇次正弦分量：

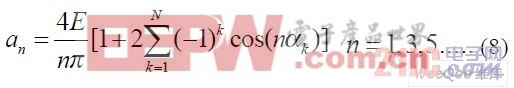
　　式中， k a 為[0，p / 2]區間內的N個開關角中的第k個開關角，n 為基波和各次諧波的次數。

　　在此令q 為所選定的基波幅值(為表示方便，進行幅值歸一化處理，即令E= 1， 則：

　　對于單相逆變器，若令n=3，5，7，9，?為擬消除的諧波次數， 則有：

　　方程(9)和方程組(10)中有N 個自變量1 2 3 ， ， ，.... N a a a a ，我們使基波幅值q 為一需要的值，并在方程組(10)中取N-1 個方程，則方程(9)和方程組(10)就構造了在四分之一周期內用N 個開關角來消除N-1 個特定諧波的特定消諧技術的數學模型。