如何提高DSP的ADC精度
F2812的ADC共有輸入通道16個,由于通道之間的誤差會在±0.2%以內,所以可以任選其中的6路通道作為校正輸入端,并分別輸入6個不相等的標準直流參考電壓。通過在程序中定義結構體變量讀取轉化后的值,得到6組輸入/輸出平面上的坐標點。然后利用最小二乘和一元線性回歸思想處理數據,求出的擬合最佳曲線,使得各個坐標點到該最佳曲線的距離的平方和(殘差平方和)最小。
2 最小二乘法和一元線性回歸
2.1 最小二乘原理
對于線性模型,如果有t個不可測量的未知量,理論上,可對與該t個未知量有函數關系的直接測量量進行t次測量,即可得到函數關系。但由于測量數據不可避免地包含著測量誤差,所得到的結果也必定含有一定的誤差。為了提高所得結果的精度,可以把測量次數增加到n(n>t),以利用抵償性減小隨機誤差的影響。
高斯認為,根據觀測數據求取未知參數時,未知參數最合適數值應是這樣的數值,即選出使得模型輸出與觀測數據盡可能接近的參數估計,接近程度用模型輸出和數據之差的平方和來度量。這就是最小二乘的基本思想。最小二乘法原理指出,最精確的值應在使殘余誤差平方和最小的條件下求得。
2.2 一元線性回歸原理
一元線性回歸是處理2個變量之間的關系,即兩個變量x和y之間若存在線性關系,則通過試驗,分析所得數據,找出兩者之間函數曲線。也就是工程上常遇到的直線擬合問題。
3 實驗方案與結果分析
3.1 實驗方案
實驗利用F2812開發板和DSP調試軟件CCS2.0完成。用穩定信號源產生6個標準電壓,分別為0.2 V,0.5 V,1.0 V,1.5 V,2.0 V,2.5 V,輸入通道選為A0,A1,A2,B0,B1,B2。ADCL0引腳接電路板的模擬地,與模擬輸入引腳相連的信號線應該避開數字信號線,以減少數字信號對模擬信號的干擾。輸入電路如圖2所示。
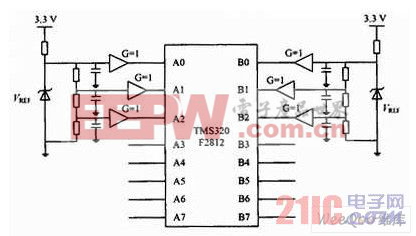
圖2 輸入電路
3.2 校正算法
設ADC模塊的輸入/輸出曲線為y=a+bx,輸入電壓值為xi,對應的轉化輸出值為yi。由最小二乘估計算法可得方程:

解此方程組即可得到a,b的估計值:
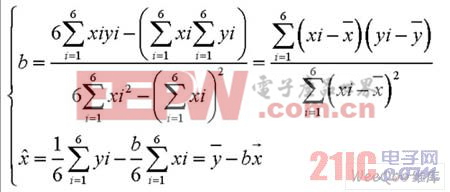
式中, 這樣這樣便得到了最佳的擬合曲線(回歸方程):
這樣這樣便得到了最佳的擬合曲線(回歸方程): 于是可以用此方程進行轉化值校正。
于是可以用此方程進行轉化值校正。








評論