基于DSP的FIR數字濾波器的實現

摘要：在數字信號處理應用中，濾波占有十分重要的地位，如對信號的過濾、檢測、預測等，都要廣泛地用到濾波器。文中研究了FIR濾波器窗函數算法的基本思想給出了在定點DSP芯片上實現FIR數字濾波器的設計方法，并給出了仿真結果。
關鍵詞：DSP；FIR濾波器；循環尋址；漢寧窗

0 引言
數字信號處理現已在通信與信息系統、信號與信息系統、自動控制、需達、軍事、航空航天、醫療和家用電器等眾多領域得到了廣泛的應用。在數字信號處理應用中，濾波占有十分重要的地位，如對信號的過濾、檢測、預測等，都要廣泛地用到濾波器。IIR數字濾波器的設計保留了一些典型模擬濾波器優良的幅度特性，但所涉及的濾波器相位特性一般是非線性的，而FIR濾波器則可在保證幅度特性并滿足技術要求的同時，也很容易做到嚴格的線性相位特性。

1 基于窗函數法的FIR濾波器設計
1．1 單位沖激響應
首先應根據技術要求確定待求濾波器的單位沖激響應hd(n)。如果給出待求濾波器的頻率為，那么單位取樣響應則可用下式求出：

當較復雜或不能用封閉公式表示時，就不能用上式求出hd(n)。此時可以對從ω=0到ω=2π采樣M個點， 采樣值為，k=0，1，2，…，M-1，并用2π/M代替(1)式中的dω，此時(1)式可近似寫成：

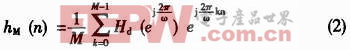
這樣，根據頻率采樣定理，hM(n)與hd(n)應滿足如下關系：

因此，如果M選得較大，就可以保證在窗口內，hM(n)有效逼近hd(n)。實際計算(2)式時，可以用的M點采樣值，來進行M點IDFT
(IFFT)，從而得到(2)式的值。
如果給出通帶阻帶衰減和邊界頻率的要求，則可選用理想濾波器作為逼近函數，從而用理想濾波器的特性作傅立葉逆變換，以求出hd(n)。若理想低通濾波器為：

那么，求出的單位取樣響應hd(n)則為：

為保證線性相位，通常應取α=(N-1)／2。