基于雙混沌映射的圖像加密算法研究

　　2.1 置換矩陣的構造

　　首先利用一種隨機全排列生成算法來生成置換加密中所需的全排列。所謂全排列即是將M個不同元素按照一定的順序排列起來，稱為這M個不同元素的一個全排列。本置換方法分為行置換和列置換，行置換算法描述如下：

　　（1）設生成的置換矩陣大小為m×n,首先要生成一個0~M-1之間的全排列元素，元素數目為M（M>n）。

　　（2）初始化全排列矩陣，令{0,1,…，M-1}中所有元素的一個全排列為{a0,a1,…，aM-1},當i≠j時，有ai≠aj.全排列初始值系數為L,令n=?WL×M」，L可以當密鑰給出，一般L在（0.5,0.7）區間即可。若太小，則產生的全排列隨機性差；若太大，則數據重復多，將會增加系統的迭代次數。

　　（3）設所用混沌系統方程為xn=f（xn-1），本文用的是Logistic混沌模型，xn即為當前混沌序列，每次都要進行迭代來產生新的混沌序列。利用不等分區間的動態量化對混沌序列進行進一步處理，以增強其隨機性和復雜度，本文利用判決公式（3）對Logistic混沌方程式（1）產生的序列{xn}進行判決，可以得到K=2n進

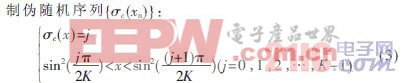
　　定義序列{xn}經過判決所在的位置構成序列為Pn={p1,p2,…，pn},其中Pi=j,即每一個xi都和一個xpi相對應，可進行兩個位置元素交換，然后再重新判決，通過這樣的量化即可得到n個0~M-1之間的隨機數。

　　（4）初始化一個數組A,初始為空，最大長度為m,將步驟（2）生成的元素依次添加到A中，若A中不存在生成的元素，則添加到A末尾，否則舍棄。直到A中元素為n個，然后將0~M-1間元素不在A中的依次添加到A中，形成初始化全排列A.

　　（5）對初始化全排列A再進行一次全變換來增強隨機性，方法同步驟（2），即將兩個對應位置元素A[Pi]同A[Ppi]的交換。這里全變換的次數可以自行設定，但考慮系統運行的速度，全變換輪數r不宜過大，一般不超過5輪，由密鑰給出。

　　（6）反復執行步驟（3）、（4）、（5）可得到一個m行隨機全排列，即可構成m×n大小的行置換矩陣A′。

　　（7）行置換方法可看作函數B=E（A′，T），其中B為加密后矩陣，即是將T[i,j]的值賦給B[i,Ppj].列置換的方法和行置換方法相同，在此不再描述。設矩陣B經過列置換后為B′m×n.

　　該算法生成的全排列對混沌系統的初值敏感，密鑰的細微差別都將產生不同的全排列。利用該算法可以生成任意多所需長度的隨機全排列，算法中細微部分可以靈活處理，以增強密鑰強度。

　　2.2異或矩陣的構造

　　利用Henon映射進行迭代產生隨機數構成異或矩陣。由于Henon映射有一定的局限性，對常用的幾種混沌模型產生的序列進行隨機性測試，得出Henon混沌映射的隨機性強度并不是十分理想。因此，本文用Henon混沌序列進行擾動變換后產生相關序列及參數，將輸出結果進行整數取余進一步量化得到異或矩陣。其中部分細節可以靈活變換修改，在此不作詳細規定。

　　（4）反復執行步驟（1）、（2）、（3），直到構成大小為m×n的異或矩陣所需隨機數，設得到的異或矩陣為Cm×n.

　　（5）將異或矩陣Cm×n與所得的置換矩陣B′m×n逐一異或即可得到加密矩陣。

　　異或矩陣的使用增強了整個算法的安全性。置換矩陣和異或矩陣的使用，進一步增強了加密效果，使抗攻擊能力得到增強。