參數化可配置IP核浮點運算器的設計與實現
參數化可配置技術是指在集成開發環境下,利用設計中的可配置資源,根據需求重新配置一個運算系統,以實現兼顧高性能硬件設計和可配置特征的系統,即成為參數化可配置運算系統。參數化可配置系統的原理是:通過對參數可配置元件的利用,將硬件系統由專門的電路設計轉變成為功能模塊的組裝,因此具有靈活、高效、低耗、易于開發與升級等特性。
在混沌電路、信號及圖像處理中有大量的浮點數加、減、乘、除操作,浮點數本身的復雜性決定其需要專用的硬件來實現[1]。傳統硬件電路的實現依靠手工搭建,過程復雜,存在電路參數分布性大、元器件老化、易受溫度影響及通用性差等問題,尤其是對網格狀多渦卷混沌吸引子的電路設計和調試需要花費更多時間。此外,要求電路設計者要有較高的技巧和經驗[2]。基于IP核模塊的設計方法是采用IP核模塊而不是采用基本邏輯或電路單元作為基礎單元,是以功能組裝代替功能設計,用戶只需通過設置參數即可方便地按需要定制自己的宏功能模塊。使用戶可以將精力集中于系統頂層及關鍵功能模塊的設計上,致力于提高產品整體性能和個性化特性,加快了芯片設計速度,提高了芯片設計能力。
此外,IP核通常要經過嚴格的測試和優化,并且已經封裝完畢,利用IP核進行電路設計可以在FPGA等可編程邏輯器件中達到最優的性能和最低的邏輯資源使用率,以保證電路的性能和質量。基于參數可配置IP核的浮點運算器的設計可大大提高混沌電路及其他電路設計者的電路設計能力,有力推動了混沌電路在相關領域的應用。
1 參數化IP核
IP核的本質特征之一是可重用性,在不同的應用場合對IP核功能、性能、面積及功耗等要求也不同,這就要求IP核具有較好的可伸縮性和靈活性。為了使IP核在使用中具有更好的靈活性和可配置性,IP核應該被設置為參數化可配置的。根據參數配置時機的不同,參數化IP核的配置參數可分為靜態參數和動態參數[3]。
(1)靜態參數:靜態參數是指在系統運行前,一次性將參數化IP核的參數配置為系統所需的某個或數個功能,這些配置好的功能,在系統運行期間不會改變,直到系統完成任務后,參數化IP核才配置成為其他功能去完成其他任務。也就是說,當硬件要重新配置參數時,系統必須先停止運行,待參數配置完成后系統才能繼續運行。
(2)動態參數:動態參數是在系統運行過程中,可隨時重新配置參數化IP核的功能,參數配置與系統運行是同時的。因此,在設計IP核的動態參數時,必須先把參數配置所需的電路模塊包含在其中,并將可配置的參數保存在寄存器中,這樣在系統運行時才能隨時配置參數調用所需的功能。圖1為動態參數的控制結構。
(3)動態參數與靜態參數的比較:動態參數的使用大大提升了IP核的運行靈活性,但其缺點也很明顯。因為動態參數屬于“運行時配置”的參數。采用動態參數設計的IP核,在設計時已經將所有的功能模塊包含在電路中,通過參數寄存器來實時選擇IP核的功能,因此,電路設計功能越多、參數越復雜,其芯片面積的占用和功耗也越大。而靜態參數屬于“編譯時配置”的參數[4],它在流片之前就已經將IP核的參數確定好,因而在實現過程中不會產生冗余電路,減小了設計成本。
2 參數化浮點運算器IP核設計
在參數化浮點運算器IP核的設計中,由于浮點減法器與浮點除法器都可通過參數化浮點加法器和參數化浮點乘法器實現,故本設計只重點探討參數化浮點加法器和參數化乘法器的優化算法和設計技術。
2.1參數化浮點加法器設計
浮點加/減法在浮點運算中占有很大的比例,在浮點加法器的設計中,尾數的計算是影響浮點運算性能的關鍵,而其中進位運算對尾數計算速度影響最大。因此,圍繞如何提高浮點運算器的進位產生速度,科研人員在傳統串行的行波進位加法器的基礎上,提出了一些并行快速產生進位的方法,如:超前進位加法器CLA(Carry Look-ahead Adder)、條件進位選擇CCS(Conditional Carry-Selection)加法器等。本文采用的是對超前進位加法器改進后的、適用于參數化浮點運算器設計的分塊超前進位加法器BCLA(Block Carry Look-ahead Adder)。
2.1.1 分塊超前進位加法器算法
圖2是一個 4 bit超前進位加法器模塊,通過將數個CLA分成相同大小分組級聯,組間采用行波進位的方式連接,以加強加法器件的模塊性。
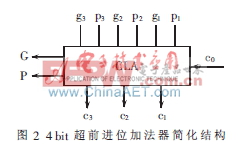

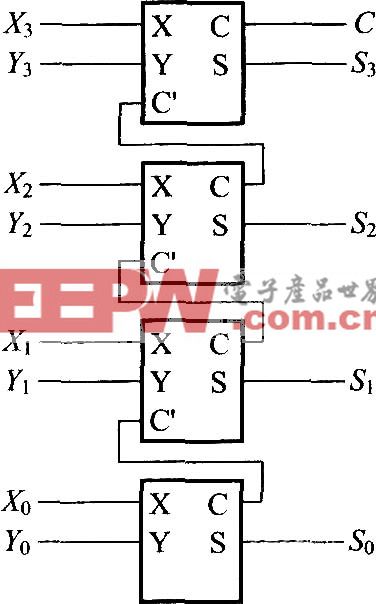
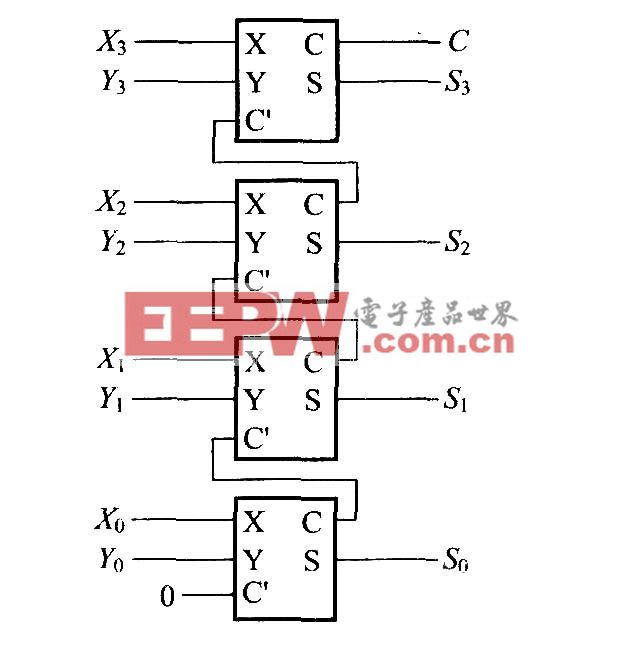
依據式(1),組間產生和傳遞的進位,可以采用相類似的方式產生,通過增加一個組間CLA以組合方式設計成為分塊超前進位加法器組合電路。圖3為采用BCLA以及CLA組合設計的16 bit加法器邏輯圖。對于n位操作數的加法,可將其分為n/4個分組,每4 bit一個CLA的模塊完成一次超前進位運算需要2ΔG的時間(假設每個門電路延遲為ΔG)。其中需要1ΔG的時間產生Pi和Gi,2ΔG的時間來產生本位輸出,因此,整個電路的總運算時間為:
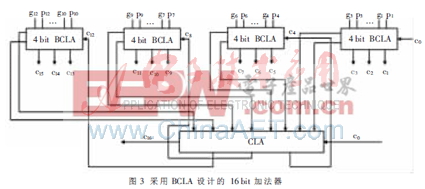
從式(2)可以看出,與完全的行波進位加法器的延遲2nΔG相比,采用BCLA方法設計的加法器的延遲理論上只有其1/4,性能得到了很大的提升。
2.1.2 分塊超前進位加法器設計
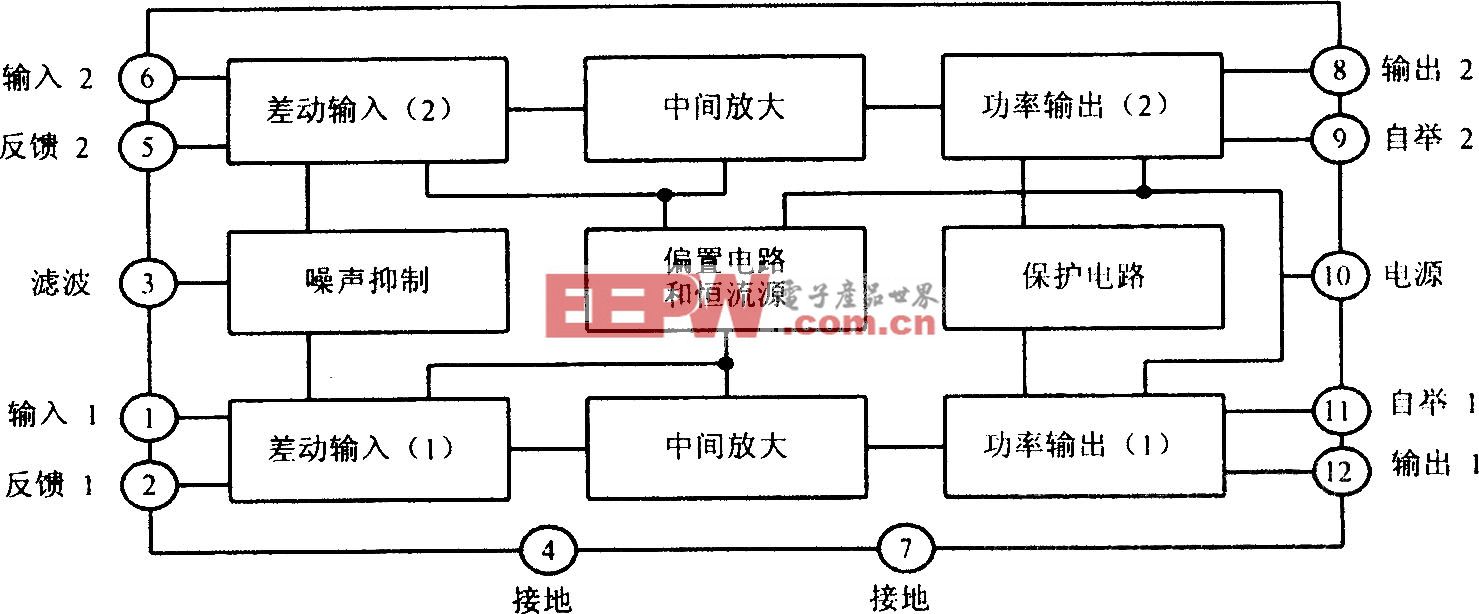
根據IEEE-754標準的浮點加/減法的基本原理[5],對于兩個浮點數的加/減法,可將其分解為8個步驟:符號運算、指數運算、尾數移位、尾數運算、規格化、指數調整、舍入、封裝。然后根據這8個步驟,對浮點加/減法進行運算的細化。在細化流程的基礎上,把尾數對位劃分為對階和移位,在符號運算電路中加入加減法操作的信號,根據IEEE-754標準的浮點格式的限制及異常處理,劃分浮點數的加/減法運算電路的功能模塊。圖4為分塊超前進位加法器的功能模塊。
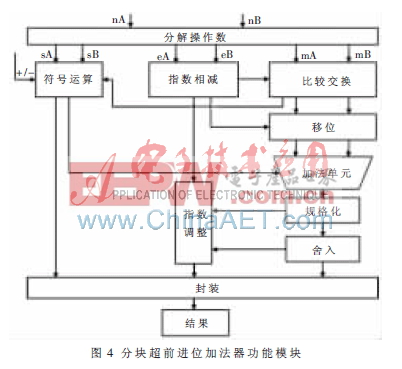
為了使基于VHDL設計的參數化IP核開發流程明確、設計目標清晰,需要在進行VHDL描述之前對浮點加法器的參數的提取進行研究,分析出可提取參數和可實現的參數。在浮點運算器中對參數的配置主要要求是:
(1) 各參數之間的耦合度應該比較小;
(2) 可進行參數配置的模塊,能夠顯著改變浮點運算器的性能、面積、功耗等;
(3) 參數化應該比較容易實現。
2.2參數化浮點乘法器設計
浮點乘法在浮點運算器中的使用比例僅次于浮點加/減法,因此也是非常關鍵的浮點運算部件之一。按照IEEE-754標準,浮點運算被分為符號位運算、指數運算、尾數相乘三個步驟,從20世紀60年代至今,已經提出了許多種定點乘法運算單元的實現方法。各種乘法器運算方式都是先將乘法轉換為加法,再通過快速求和的方法來得到最終的計算結果。本文采用的是適用于參數化浮點運算器設計的Booth算法。
(1)為解決有符號數乘法運算中復雜的符號修正問題,Booth提出了一種針對乘數進行編碼的Booth編碼。Booth編碼在乘數最低位增加一個零值,在循環求部分積時,每次取乘數的相鄰兩位(基-4)進行判斷,依據這兩位的值,判斷其部分積是被乘數的一倍或是兩倍[6]。
Booth編碼乘法運算可分三步進行:①產生部分積;②加法陣列累加部分積;③應用加法器求得最終結果。
采用Booth編碼設計的乘法器原理如圖5所示。




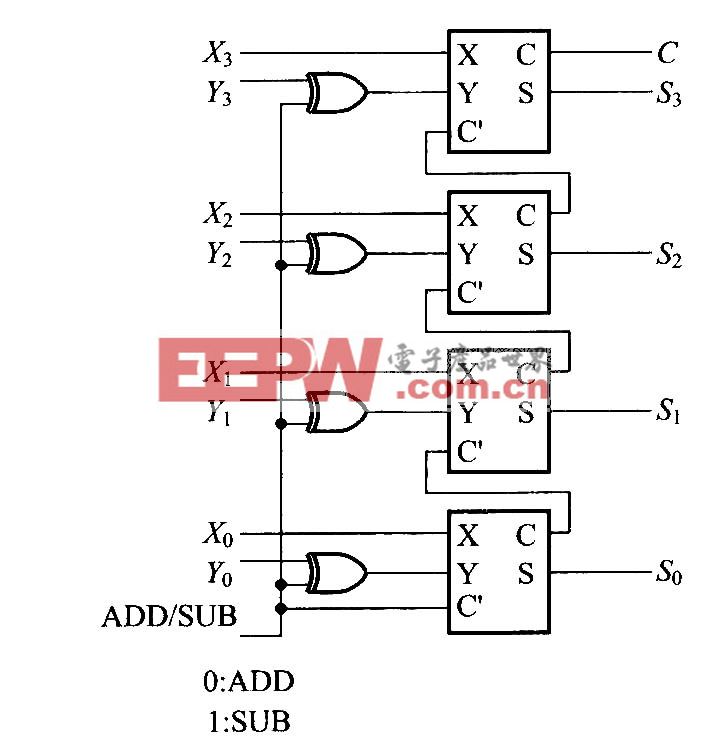




評論