篩子的點數，是隨機的嗎？

打開微信，往一個8人群里發一個9分錢的拼手氣紅包。那么不管你發多少次，最后一個搶紅包的人都必定能拿到兩分錢，不信你可以試一試。顯然，在分配紅包金額這件事上，你手上的這臺小型計算機并不是真的隨機。那計算機是如何制造隨機事件的？各種軟件中的隨機都是真的隨機嗎？

在計算機中生成隨機事件的關鍵是輸出一個隨機數，然后再利用算法就能模擬出各式各樣的隨機事件。你剛才看到的拼手氣紅包背后就有這樣一套算法。其中的隨機數決定了你最后搶到的金額大小。如何才能得到這樣的隨機數呢？

1946年，計算機支付馮諾依曼提出了這么一套方案，編寫一個隨機數生成器，只要輸入任意一個數字作為種子，計算機就能通過運算生成一個新的隨機數字。然后再把這個數字作為輸入值帶入下一輪計算，重復這個過程，就能生成多個具有統計意義的隨機數。

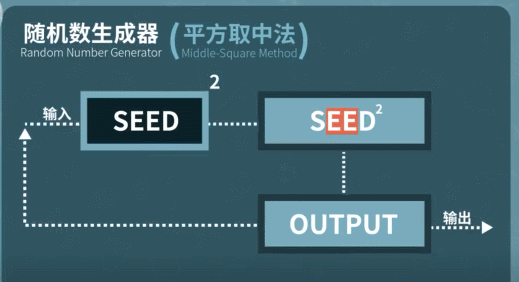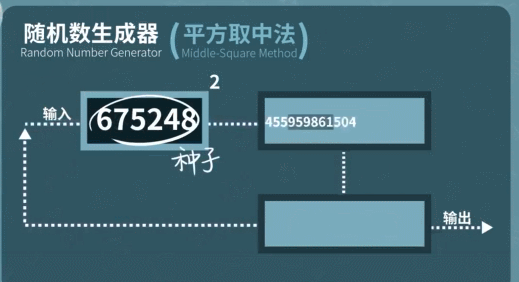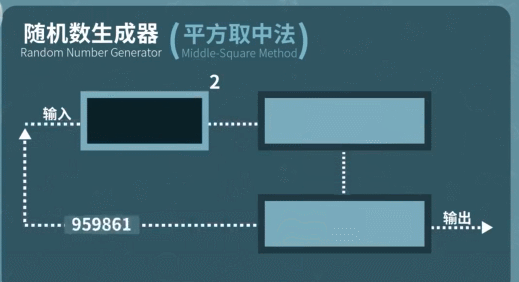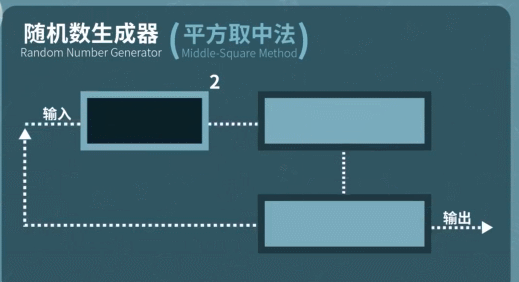
直到今天，你的手機電腦仍然在沿用這套隨機數生成方案，只是把隨機數生成器升級成了運算效果更好的線性反饋移位寄存器。隨機種子的花樣也更多了。從系統時間、鼠標位置到網絡速度，硬盤讀寫速度，甚至是你聊天記錄的本地文件都可以被拿來當做隨機數生成的初始條件，決定最后的隨機結果。這樣得到的數字，乍看起來非常隨機。但受到算法的限制，只要取樣范圍夠大，數字排列早晚會陷入循環。所以這種方式產生的隨機數只能叫做偽隨機數。

以常用的梅森旋轉算法為例，它生成隨機數的循環周期是2的19937次方。哪怕全世界的計算機一起工作，直到太陽系毀滅的那一天，你也等不到這個循環。但無論循環周期有多長，只要知道一開始的隨機種子，再用同一個隨機數生成器，就能預測隨機結果。

比如在1994年，飛利浦的一名員工就弄到了當時的互聯網巨頭Netscape的服務器隨機種子，在輸入當前時間加特定字符之后，他就成功解密了對方所有網絡服務器的流量信息。

除了能完美預測偽隨機結果，你甚至還能主動改變隨機種子的數值，讓所謂的隨機事件變成百分之百發生的必然事件。

比如2014年，俄羅斯的一位數學家就拆解了一臺舊老虎機，獲取了老虎機采用的偽隨機算法，然后設計了一套程序，只要用手機拍下其他人的****博過程，就能反推計算出老虎機所用的隨機種子。有了這套方法，你只需要找出對應時間點拉下拉桿就能歐神附體，百發百中。最終被丟出****場關進局子。

說到底，雖然偽隨機數應用廣泛，但它畢竟不是真正的隨機數，想要生成無法預測的真隨機數，還得從硬件層面想辦法。1999年，英特爾在其i810芯片組上集成了一枚真隨機數生成器。它通過放大電路產生的熱噪聲，把電路中分子的不規則熱運動作為數據來源，這才讓計算機擁有了自主生成隨機數的能力。類似的一些專門提供真隨機數服務的公司，還會通過收集現實世界中的隨機事件，比如大氣噪音的振幅變化，或者是人工擲骰子轉動輪盤的結果。再把它們轉化為二進制或者十進制的數字，以此獲得更高品質的隨機數資源。通過這些方式獲得的隨機數幾乎不可能預測，所以被稱為真隨機數。他們主要被應用于安全或者密碼學領域，用來保護最重要的數據信息。

不過如果硬要抬杠，那么這種真隨機數其實也不夠隨機。因為宏觀現實世界里的一切隨機現象仍然遵循物理學的必然規律，只是我們這些凡人無法參透罷了。如果拉普拉斯妖真的存在，那么理論上它就能知曉所有原子的分布和動量，算出任何色子的點數，破解一切加密的信息。如果想要實現絕對的隨機，那就只能求助于量子力學了。

隨著技術發展，如今的研究人員已經能夠通過記錄元素的衰變和放射情況，或者是探測真空中氬原子的噪音，或者統計出糾纏粒子出現的隨機位，設計出更新型的隨機數生成器。

在現有科學體系下，這種方式產生的數字沒有規律，在物理和哲學層面上都絕對不可預測，是真正意義上的隨機數。不過回歸現實，用量子力學生成隨機數，技術難度實在太高，用芯片自帶的真隨機數生成器，輸出效率又太低。

你手上這臺計算機現在用的，其實還是尾隨基數。而且有時候過于隨機，也不一定是件好事兒。如果沒有軟件算法為用戶把控恰到好處的隨機感，而是直接讓這些隨機數來決定結果。那么你很可能在聽音樂的時候，連續三次都聽到同一首曲子。搶紅包的時候，每一次都是手氣最差。玩游戲的時候連抽一百張卡都沒有SSR。說白了，你感受到的隨機根本就不是命運的捉弄，而是算法提前安排好的罷了。