『帶你學AI』一文帶你搞懂OCR識別算法CRNN：解析+源碼

以下文章來源于極簡AI ，作者小宋是呢

前言

文字識別是AI的一個重要應用場景，文字識別過程一般由圖像輸入、預處理、文本檢測、文本識別、結果輸出等環節組成。

其中，文本檢測、文本識別是最核心的環節。文本檢測方面，在我的 OCR_detection 專欄相關文章中已介紹過了多種基于深度學習的方法（有的還沒完成，待整理后都會放入該專欄），可針對各種場景實現對文字的檢測，詳請見專欄中的相關文章。

在以前的 OCR 任務中，識別過程分為兩步：單字切割 和 分類任務。我們一般都會將一連串文字的文本文件先利用 投影法 切割出單個字體，再送入 CNN 里進行文字分類。但是此法已經有點過時了，現在更流行的是基于深度學習的端到端的文字識別，即我們不需要顯式加入文字切割這個環節，而是將文字識別轉化為序列學習問題，雖然輸入的圖像尺度不同，文本長度不同，但是經過 DCNN 和 RNN 后，在輸出階段經過一定的 CTC 翻譯轉錄后，就可以對整個文本圖像進行識別，也就是說，文字的切割也被融入到深度學習中去了。

現今基于深度學習的端到端 OCR 技術有兩大主流技術：CRNN OCR 和 attention OCR。其實這兩大方法主要區別在于最后的輸出層（翻譯層），即怎么將網絡學習到的序列特征信息轉化為最終的識別結果。這兩大主流技術在其特征學習階段都采用了 CNN+RNN 的網絡結構，CRNN OCR 在對齊時采取的方式是 CTC 算法，而 attention OCR 采取的方式則是 attention 機制。本部分主要介紹應用更為廣泛的 CRNN 算法。

02 CRNN 介紹

CRNN 模型，即將 CNN 與 RNN 網絡結合，共同訓練。主要用于在一定程度上實現端到端（end-to-end）地對不定長的文本序列進行識別，不用先對單個文字進行切割，而是將文本識別轉化為時序依賴的序列學習問題，就是基于圖像的序列識別。（說一定程度是因為雖然輸入圖像不需要精確給出每個字符的位置信息，但實際上還是需要對原始的圖像進行前期的裁切工作）

• 構建 CRNN 輸入特征序列；

• 其中還涉及到了 CTC 模塊，目的是對其輸入輸出結果

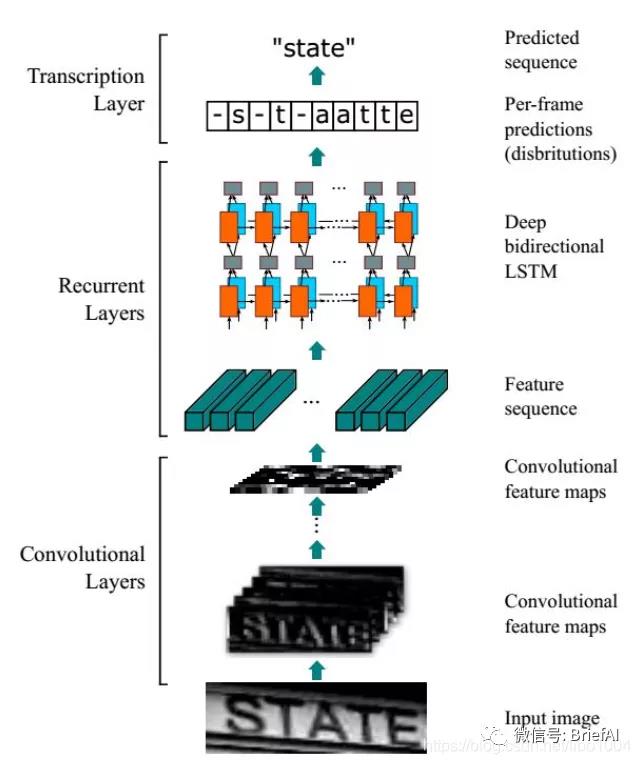
整個CRNN網絡結構包含三部分，從下到上依次為：

• CNN（卷積層）：使用深度 CNN，對輸入圖像提取特征，得到特征圖；

• RNN（循環層）：使用 雙向RNN（BLSTM）對特征序列進行預測，對序列中的每個特征向量進行學習，并輸出預測標簽（真實值）分布；

• CTC loss（轉錄層）：使用 CTC 損失，把從循環層獲取的一系列標簽分布轉換成最終的標簽序列。

03 CRNN 網絡結構

1.CNN

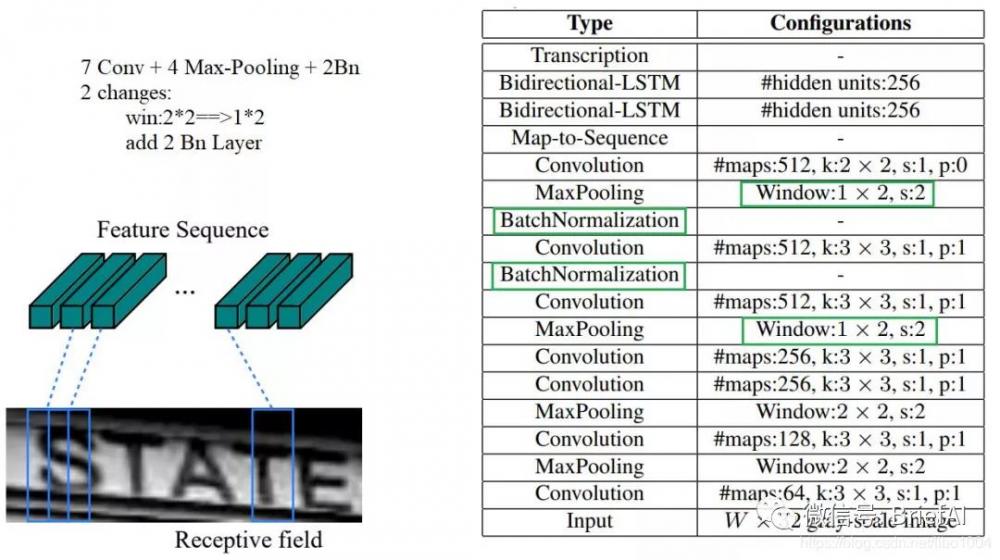
這里有一個很精彩的改動，一共有四個最大池化層，但是最后兩個池化層的窗口尺寸由 2x2 改為 1x2，也就是圖片的高度減半了四次（除以 2 4 2^424），而寬度則只減半了兩次（除以 2 2 2^222），這是因為文本圖像多數都是高較小而寬較長，所以其 feature map 也是這種高小寬長的矩形形狀，如果使用 1×2 的池化窗口可以盡量保證不丟失在寬度方向的信息，更適合英文字母識別（比如區分 i 和 l）。

CRNN 還引入了 Batch Normalization 模塊，加速模型收斂，縮短訓練過程。

例如：

輸入圖像為灰度圖像（單通道）；

高度為32，這是固定的，圖片通過 CNN 后，高度就變為 1，這點很重要；

寬度為160，寬度也可以為其他的值，但需要統一，所以輸入 CNN 的數據尺寸為 (channel, height, width)=(1, 32, 160)。

CNN 的輸出尺寸為 (512, 1, 40)。即 CNN 最后得到 512 個特征圖，每個特征圖的高度為 1，寬度為 40。

注意：最后的卷積層是一個 2*2, s=1, p=0 的卷積，此時也是相當于將 feature map 放縮為原來的 1/2,所以整個 CNN 層將圖像的 h 放縮為原來的1/(2^4)*2 = 1/32，所以最后 CNN 輸出的 feature map 的高度為1。assert imgH % 16 == 0, 'imgH has to be a multiple of 16'

在程序中，圖像的 h 必須為 16 的整數倍。assert h == 1, "the height of conv must be 1"

前向傳播時，CNN 得到的 feature map 的 h 必須為 1。

最后 CNN 得到的 feature map 尺度為 512x1x16

2.Map-to-Sequence

不能直接把 CNN 得到的特征圖送入 RNN 進行訓練的，需要進行一些調整，根據特征圖提取 RNN 需要的特征向量序列。

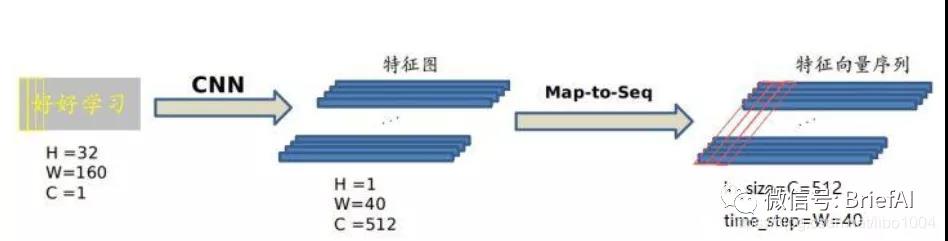
現在需要從 CNN 模型產生的特征圖中提取特征向量序列，每一個特征向量（如上圖中的一個紅色框）在特征圖上 按列 從左到右生成，每一列包含 512 維特征，這意味著第 i 個特征向量是所有的特征圖第 i 列像素的連接，這些特征向量就構成一個序列。

由于卷積層，最大池化層和激活函數在局部區域上執行，因此它們是平移不變的。因此，特征圖的每列（即一個特征向量）對應于原始圖像的一個矩形區域（稱為感受野），并且這些矩形區域與特征圖上從左到右的相應列具有相同的順序。特征序列中的每個向量關聯一個感受野。如下圖所示：

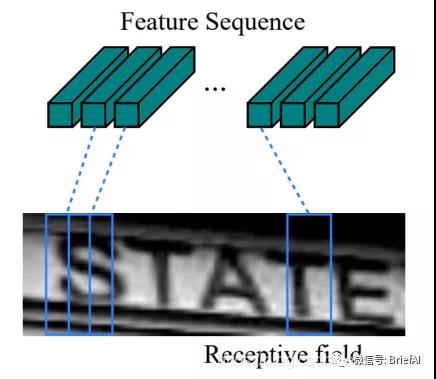
這些特征向量序列就作為循環層的輸入，每個特征向量作為 RNN 在一個時間步（time step）的輸入。

3.RNN

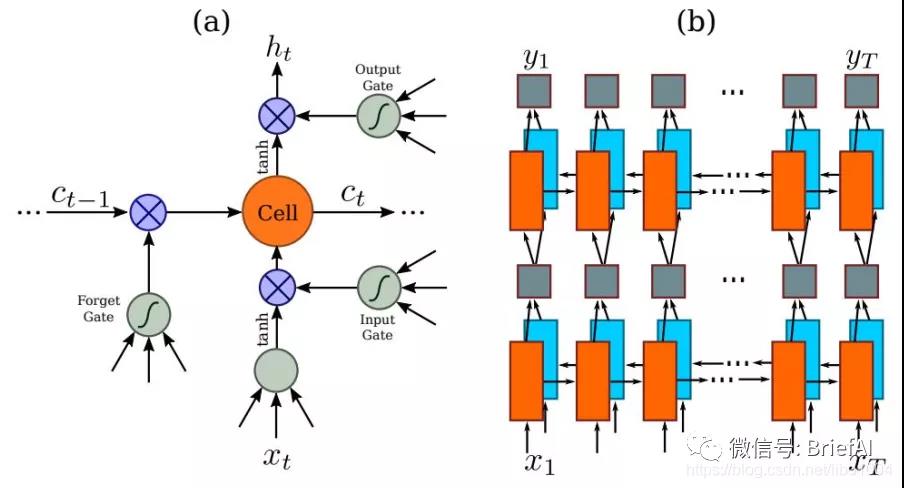
因為 RNN 有梯度消失的問題，不能獲取更多上下文信息，所以 CRNN 中使用的是 LSTM，LSTM 的特殊設計允許它捕獲長距離依賴。

LSTM 是單向的，它只使用過去的信息。然而，在基于圖像的序列中，兩個方向的上下文是相互有用且互補的。將兩個 LSTM，一個向前和一個向后組合到一個雙向 LSTM 中。此外，可以堆疊多層雙向 LSTM，深層結構允許比淺層抽象更高層次的抽象。

這里采用的是兩層各 256 單元的雙向 LSTM 網絡：

通過上面一步，我們得到了 40 個特征向量，每個特征向量長度為 512，在 LSTM 中一個時間步就傳入一個特征向量進行分類，這里一共有 40 個時間步。

我們知道一個特征向量就相當于原圖中的一個小矩形區域，RNN 的目標就是預測這個矩形區域為哪個字符，即根據輸入的特征向量，進行預測，得到所有字符的 softmax 概率分布，這是一個長度為字符類別數的向量，作為 CTC 層的輸入。

因為每個時間步都會有一個輸入特征向量 x t x_txt，輸出一個所有字符的概率分布 y t y_tyt，所以輸出為 40 個長度為字符類別數的向量構成的后驗概率矩陣。如下圖所示：

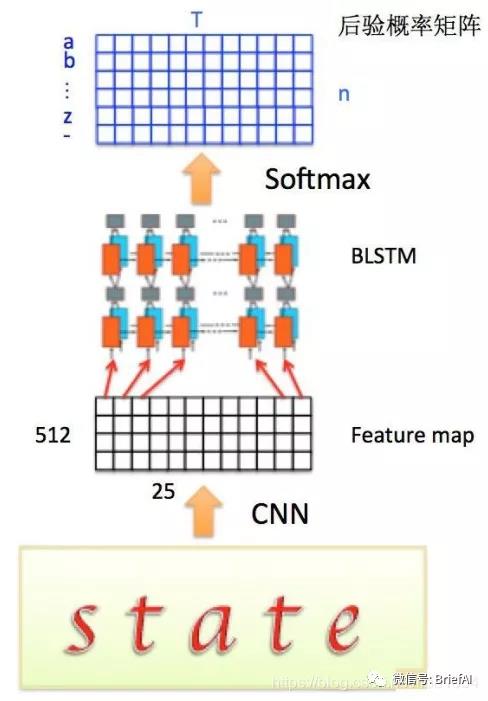
然后將這個后驗概率矩陣傳入轉錄層。

該部分的源碼如下：

self.rnn = nn.Sequential(

    BidirectionalLSTM(512, nh, nh),

    BidirectionalLSTM(nh, nh, nclass)

)

然后參數設置如下：

nh = 256

nclass = len(opt.alphabet) + 1

nc = 1

其中 BLSTM 的實現如下：

class BidirectionalLSTM(nn.Module):

def __init__(self, nIn, nHidden, nOut):

    super(BidirectionalLSTM, self).__init__()

    self.rnn = nn.LSTM(nIn, nHidden, bidirectional=True)

    self.embedding = nn.Linear(nHidden * 2, nOut)

def forward(self, input):

    recurrent, _ = self.rnn(input)

    T, b, h = recurrent.size()

    t_rec = recurrent.view(T * b, h)

    output = self.embedding(t_rec)  # [T * b, nOut]

    output = output.view(T, b, -1)

    return output

所以第一次 LSTM 得到的 output=[40*256,256]，然后 view 成 output=[40,256,256]

第二次 LSTM 得到的結果是 output=[40*256,nclass]，然后 view 成 output=[40,256,nclass]

4.CTC Loss

這算是 CRNN 最難的地方，這一層為轉錄層，轉錄是將 RNN 對每個特征向量所做的預測轉換成標簽序列的過程。數學上，轉錄是根據每幀預測找到具有最高概率組合的標簽序列。

端到端 OCR 識別的難點在于怎么處理不定長序列對齊的問題！OCR 可建模為時序依賴的文本圖像問題，然后使用 CTC（Connectionist Temporal Classification, CTC）的損失函數來對 CNN 和 RNN 進行端到端的聯合訓練。

4.1 序列合并機制

我們現在要將 RNN 輸出的序列翻譯成最終的識別結果，RNN 進行時序分類時，不可避免地會出現很多冗余信息，比如一個字母被連續識別兩次，這就需要一套去冗余機制。

比如我們要識別上面這個文本，其中 RNN 中有 5 個時間步，理想情況下 t0, t1, t2 時刻都應映射為 “a”，t3, t4 時刻都應映射為 “b”，然后將這些字符序列連接起來得到 “aaabb”，我們再將連續重復的字符合并成一個，那么最終結果為 “ab”。

這似乎是個比較好的方法，但是存在一個問題，如果是 book，hello 之類的詞，合并連續字符后就會得到 bok 和 helo，這顯然不行，所以 CTC 有一個 blank 機制來解決這個問題。

我們以 “-” 符號代表 blank，RNN 輸出序列時，在文本標簽中的重復的字符之間插入一個 “-”，比如輸出序列為 “bbooo-ookk”，則最后將被映射為 “book”，即有 blank 字符隔開的話，連續相同字符就不進行合并。

即對字符序列先刪除連續重復字符，然后從路徑中刪除所有 “-” 字符，這個稱為解碼過程，而編碼則是由神經網絡來實現。引入 blank 機制，我們就可以很好地解決重復字符的問題。

相同的文本標簽可以有多個不同的字符對齊組合，例如，“aa-b” 和 “aabb” 以及 “-abb” 都代表相同的文本 (“ab”)，但是與圖像的對齊方式不同。更總結地說，一個文本標簽存在一條或多條的路徑。

4.2 訓練階段

在訓練階段，我們需要根據這些概率分布向量和相應的文本標簽得到損失函數，從而訓練神經網路模型，下面來看看如何得到損失函數的。

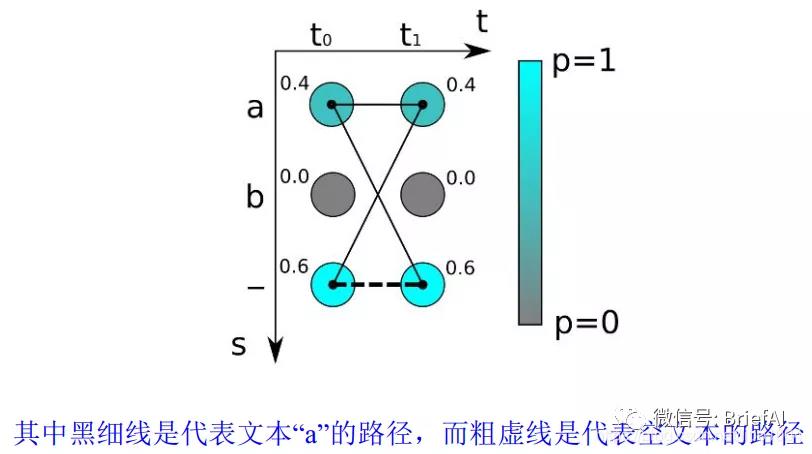
如上圖，對于最簡單的時序為 2 的字符識別，有兩個時間步長 (t0，t1) 和三個可能的字符為 “ａ”，“ｂ” 和 “-”，我們得到兩個概率分布向量，如果采取最大概率路徑解碼的方法，則 “--” 的概率最大，即真實字符為空的概率為 0.6*0.6=0.36。

但是為字符 “ａ” 的情況有多種對齊組合，“aa”, “a-“ 和 “-a” 都是代表 “ａ”，所以，輸出 “ａ” 的概率應該為三種之和：

所以 “ａ” 的概率比空 “-” 的概率高！如果標簽文本為 “a”，則通過計算圖像中為 “a” 的所有可能的對齊組合（或者路徑）的分數之和來計算損失函數。

所以對于 RNN 給定輸入概率分布矩陣為 y={y1,y2,…,yT}，T是序列長度，最后映射為標簽文本l的總概率為：

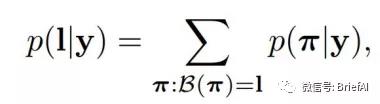
其中 B(π) 代表從序列到序列的映射函數 B 變換后是文本 l 的所有路徑集合，而 π 則是其中的一條路徑。每條路徑的概率為各個時間步中對應字符的分數的乘積。

我們就是需要訓練網絡使得這個概率值最大化，類似于普通的分類，CTC 的損失函數定義為概率的負最大似然函數，為了計算方便，對似然函數取對數。

通過對損失函數的計算，就可以對之前的神經網絡進行反向傳播，神經網絡的參數根據所使用的優化器進行更新，從而找到最可能的像素區域對應的字符。

這種通過映射變換和所有可能路徑概率之和的方式使得 CTC 不需要對原始的輸入字符序列進行準確的切分。

4.3 測試階段

在測試階段與訓練階段有所不同，我們用訓練好的神經網絡來識別新的文本圖像。這時候我們事先不知道任何文本，如果我們像上面一樣將每種可能文本的所有路徑計算出來，對于很長的時間步和很長的字符序列來說，這個計算量是非常龐大的，這不是一個可行的方案。

我們知道 RNN 在每一個時間步的輸出為所有字符類別的概率分布，即一個包含每個字符分數的向量，我們取其中最大概率的字符作為該時間步的輸出字符，然后將所有時間步得到一個字符進行拼接得到一個序列路徑，即最大概率路徑，再根據上面介紹的合并序列方法得到最終的預測文本結果。

在輸出階段經過 CTC 的翻譯，即將網絡學習到的序列特征信息轉化為最終的識別文本，就可以對整個文本圖像進行識別。

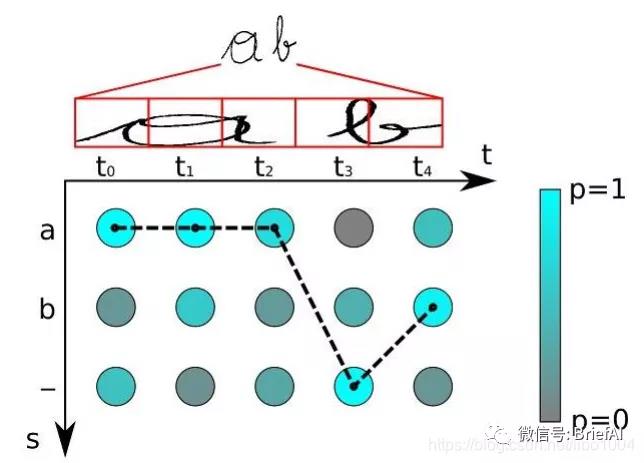
比如上面這個圖，有 5 個時間步，字符類別有 “a”, “b” and “-” (blank)，對于每個時間步的概率分布，我們都取分數最大的字符，所以得到序列路徑 “aaa-b”，先移除相鄰重復的字符得到 “a-b”，然后去除 blank 字符得到最終結果：“ab”。

04 CRNN 小結

預測過程中，先使用標準的 CNN 網絡提取文本圖像的特征，再利用 BLSTM 將特征向量進行融合以提取字符序列的上下文特征，然后得到每列特征的概率分布，最后通過 CTC 進行預測得到文本序列。

利用 BLSTM 和 CTC 學習到文本圖像中的上下文關系，從而有效提升文本識別準確率，使得模型更加魯棒。

在訓練階段，CRNN 將訓練圖像統一縮放為 w×32（w×h）；在測試階段，針對字符拉伸會導致識別率降低的問題，CRNN保持輸入圖像尺寸比例，但是圖像高度還是必須統一為 32 個像素，卷積特征圖的尺寸動態決定 LSTM 的時序長度（時間步長）。

05 CRNN 網絡模型搭建

import torch.nn as nn

from collections import OrderedDict

class BidirectionalLSTM(nn.Module):

   def __init__(self, nIn, nHidden, nOut):

       super(BidirectionalLSTM, self).__init__()

       self.rnn = nn.LSTM(nIn, nHidden, bidirectional=True)

       self.embedding = nn.Linear(nHidden * 2, nOut)

   def forward(self, input):

       recurrent, _ = self.rnn(input)

       T, b, h = recurrent.size()

       t_rec = recurrent.view(T * b, h)

       output = self.embedding(t_rec)  # [T * b, nOut]

       output = output.view(T, b, -1)

       return output

class CRNN(nn.Module):

   def __init__(self, imgH, nc, nclass, nh, leakyRelu=False):

       super(CRNN, self).__init__()

       assert imgH % 16 == 0, 'imgH has to be a multiple of 16'

       # 1x32x128

       self.conv1 = nn.Conv2d(nc, 64, 3, 1, 1)

       self.relu1 = nn.ReLU(True)

       self.pool1 = nn.MaxPool2d(2, 2)

       # 64x16x64

       self.conv2 = nn.Conv2d(64, 128, 3, 1, 1)

       self.relu2 = nn.ReLU(True)

       self.pool2 = nn.MaxPool2d(2, 2)

       # 128x8x32

       self.conv3_1 = nn.Conv2d(128, 256, 3, 1, 1)

       self.bn3 = nn.BatchNorm2d(256)

       self.relu3_1 = nn.ReLU(True)

       self.conv3_2 = nn.Conv2d(256, 256, 3, 1, 1)

       self.relu3_2 = nn.ReLU(True)

       self.pool3 = nn.MaxPool2d((2, 2), (2, 1), (0, 1))

       # 256x4x16

       self.conv4_1 = nn.Conv2d(256, 512, 3, 1, 1)

       self.bn4 = nn.BatchNorm2d(512)

       self.relu4_1 = nn.ReLU(True)

       self.conv4_2 = nn.Conv2d(512, 512, 3, 1, 1)

       self.relu4_2 = nn.ReLU(True)

       self.pool4 = nn.MaxPool2d((2, 2), (2, 1), (0, 1))

       # 512x2x16

       self.conv5 = nn.Conv2d(512, 512, 2, 1, 0)

       self.bn5 = nn.BatchNorm2d(512)

       self.relu5 = nn.ReLU(True)

       # 512x1x16

       self.rnn = nn.Sequential(

           BidirectionalLSTM(512, nh, nh),

           BidirectionalLSTM(nh, nh, nclass))

   def forward(self, input):

       # conv features

       x = self.pool1(self.relu1(self.conv1(input)))

       x = self.pool2(self.relu2(self.conv2(x)))

       x = self.pool3(self.relu3_2(self.conv3_2(self.relu3_1(self.bn3(self.conv3_1(x))))))

       x = self.pool4(self.relu4_2(self.conv4_2(self.relu4_1(self.bn4(self.conv4_1(x))))))

       conv = self.relu5(self.bn5(self.conv5(x)))

       # print(conv.size())

       b, c, h, w = conv.size()

       assert h == 1, "the height of conv must be 1"

       conv = conv.squeeze(2)

       conv = conv.permute(2, 0, 1)  # [w, b, c]

       # rnn features

       output = self.rnn(conv)

       return output

class CRNN_v2(nn.Module):

   def __init__(self, imgH, nc, nclass, nh, leakyRelu=False):

       super(CRNN_v2, self).__init__()

       assert imgH % 16 == 0, 'imgH has to be a multiple of 16'

       # 1x32x128

       self.conv1_1 = nn.Conv2d(nc, 32, 3, 1, 1)

       self.bn1_1 = nn.BatchNorm2d(32)

       self.relu1_1 = nn.ReLU(True)

       self.conv1_2 = nn.Conv2d(32, 64, 3, 1, 1)

       self.bn1_2 = nn.BatchNorm2d(64)

       self.relu1_2 = nn.ReLU(True)

       self.pool1 = nn.MaxPool2d(2, 2)

       # 64x16x64

       self.conv2_1 = nn.Conv2d(64, 64, 3, 1, 1)

       self.bn2_1 = nn.BatchNorm2d(64)

       self.relu2_1 = nn.ReLU(True)

       self.conv2_2 = nn.Conv2d(64, 128, 3, 1, 1)

       self.bn2_2 = nn.BatchNorm2d(128)

       self.relu2_2 = nn.ReLU(True)

       self.pool2 = nn.MaxPool2d(2, 2)

       # 128x8x32

       self.conv3_1 = nn.Conv2d(128, 96, 3, 1, 1)

       self.bn3_1 = nn.BatchNorm2d(96)

       self.relu3_1 = nn.ReLU(True)

       self.conv3_2 = nn.Conv2d(96, 192, 3, 1, 1)

       self.bn3_2 = nn.BatchNorm2d(192)

       self.relu3_2 = nn.ReLU(True)

       self.pool3 = nn.MaxPool2d((2, 2), (2, 1), (0, 1))

       # 192x4x32

       self.conv4_1 = nn.Conv2d(192, 128, 3, 1, 1)

       self.bn4_1 = nn.BatchNorm2d(128)

       self.relu4_1 = nn.ReLU(True)

       self.conv4_2 = nn.Conv2d(128, 256, 3, 1, 1)

       self.bn4_2 = nn.BatchNorm2d(256)

       self.relu4_2 = nn.ReLU(True)

       self.pool4 = nn.MaxPool2d((2, 2), (2, 1), (0, 1))

       # 256x2x32

       self.bn5 = nn.BatchNorm2d(256)

       # 256x2x32

       self.rnn = nn.Sequential(

           BidirectionalLSTM(512, nh, nh),

           BidirectionalLSTM(nh, nh, nclass))

   def forward(self, input):

       # conv features

       x = self.pool1(self.relu1_2(self.bn1_2(self.conv1_2(self.relu1_1(self.bn1_1(self.conv1_1(input)))))))

       x = self.pool2(self.relu2_2(self.bn2_2(self.conv2_2(self.relu2_1(self.bn2_1(self.conv2_1(x)))))))

       x = self.pool3(self.relu3_2(self.bn3_2(self.conv3_2(self.relu3_1(self.bn3_1(self.conv3_1(x)))))))

       x = self.pool4(self.relu4_2(self.bn4_2(self.conv4_2(self.relu4_1(self.bn4_1(self.conv4_1(x)))))))

       conv = self.bn5(x)

       # print(conv.size())

       b, c, h, w = conv.size()

       assert h == 2, "the height of conv must be 2"

       conv = conv.reshape([b,c*h,w])

       conv = conv.permute(2, 0, 1)  # [w, b, c]

       # rnn features

       output = self.rnn(conv)

       return output

def conv3x3(nIn, nOut, stride=1):

   # "3x3 convolution with padding"

   return nn.Conv2d( nIn, nOut, kernel_size=3, stride=stride, padding=1, bias=False )

class basic_res_block(nn.Module):

   def __init__(self, nIn, nOut, stride=1, downsample=None):

       super( basic_res_block, self ).__init__()

       m = OrderedDict()

       m['conv1'] = conv3x3( nIn, nOut, stride )

       m['bn1'] = nn.BatchNorm2d( nOut )

       m['relu1'] = nn.ReLU( inplace=True )

       m['conv2'] = conv3x3( nOut, nOut )

       m['bn2'] = nn.BatchNorm2d( nOut )

       self.group1 = nn.Sequential( m )

       self.relu = nn.Sequential( nn.ReLU( inplace=True ) )

       self.downsample = downsample

   def forward(self, x):

       if self.downsample is not None:

           residual = self.downsample( x )

       else:

           residual = x

       out = self.group1( x ) + residual

       out = self.relu( out )

       return out

class CRNN_res(nn.Module):

   def __init__(self, imgH, nc, nclass, nh):

       super(CRNN_res, self).__init__()

       assert imgH % 16 == 0, 'imgH has to be a multiple of 16'

       self.conv1 = nn.Conv2d(nc, 64, 3, 1, 1)

       self.relu1 = nn.ReLU(True)

       self.res1 = basic_res_block(64, 64)

       # 1x32x128

       down1 = nn.Sequential(nn.Conv2d(64, 128, kernel_size=1, stride=2, bias=False),nn.BatchNorm2d(128))

       self.res2_1 = basic_res_block( 64, 128, 2, down1 )

       self.res2_2 = basic_res_block(128,128)

       # 64x16x64

       down2 = nn.Sequential(nn.Conv2d(128, 256, kernel_size=1, stride=2, bias=False),nn.BatchNorm2d(256))

       self.res3_1 = basic_res_block(128, 256, 2, down2)

       self.res3_2 = basic_res_block(256, 256)

       self.res3_3 = basic_res_block(256, 256)

       # 128x8x32

       down3 = nn.Sequential(nn.Conv2d(256, 512, kernel_size=1, stride=(2, 1), bias=False),nn.BatchNorm2d(512))

       self.res4_1 = basic_res_block(256, 512, (2, 1), down3)

       self.res4_2 = basic_res_block(512, 512)

       self.res4_3 = basic_res_block(512, 512)

       # 256x4x16

       self.pool = nn.AvgPool2d((2, 2), (2, 1), (0, 1))

       # 512x2x16

       self.conv5 = nn.Conv2d(512, 512, 2, 1, 0)

       self.bn5 = nn.BatchNorm2d(512)

       self.relu5 = nn.ReLU(True)

       # 512x1x16

       self.rnn = nn.Sequential(

           BidirectionalLSTM(512, nh, nh),

           BidirectionalLSTM(nh, nh, nclass))

   def forward(self, input):

       # conv features

       x = self.res1(self.relu1(self.conv1(input)))

       x = self.res2_2(self.res2_1(x))

       x = self.res3_3(self.res3_2(self.res3_1(x)))

       x = self.res4_3(self.res4_2(self.res4_1(x)))

       x = self.pool(x)

       conv = self.relu5(self.bn5(self.conv5(x)))

       # print(conv.size())

       b, c, h, w = conv.size()

       assert h == 1, "the height of conv must be 1"

       conv = conv.squeeze(2)

       conv = conv.permute(2, 0, 1)  # [w, b, c]

       # rnn features

       output = self.rnn(conv)

       return output

if __name__ == '__main__':

   pass

參考鏈接

https://blog.csdn.net/wa1tzy/article/details/107357911

https://blog.csdn.net/qq_24819773/article/details/104605994

https://mp.weixin.qq.com/s/p801KZ5kv5aYnLvlahFlnA