AlphaGo原來是這樣運行的，一文詳解多智能體強化學習的基礎和應用（上）

在這篇綜述性文章中，作者詳盡地介紹了多智能強化學習的理論基礎，并闡述了解決各類多智能問題的經典算法。此外，作者還以 AlphaGo、AlphaStar 為例，概述了多智能體強化學習的實際應用。

近年來，隨著強化學習（reinforcement learning）在多個應用領域取得了令人矚目的成果，并且考慮到在現實場景中通常會同時存在多個決策個體（智能體），部分研究者逐漸將眼光從單智能體領域延伸到多智能體。

本文將首先簡要地介紹多智能體強化學習（multi-agent reinforcement learning, MARL）的相關理論基礎，包括問題的定義、問題的建模，以及涉及到的核心思想和概念等。然后，根據具體應用中智能體之間的關系，將多智能體問題分為完全合作式、完全競爭式、混合關系式三種類型，并簡要闡述解決各類多智能體問題的經典算法。最后，本文列舉深度強化學習在多智能體研究工作中提出的一些方法（multi-agent deep reinforcement learning）。

1. 強化學習和多智能體強化學習

我們知道，強化學習的核心思想是“試錯”（trial-and-error）：智能體通過與環境的交互，根據獲得的反饋信息迭代地優化。在 RL 領域，待解決的問題通常被描述為馬爾科夫決策過程。

圖 1：強化學習的框架（同時也表示了馬爾科夫決策過程）。圖源：[1]

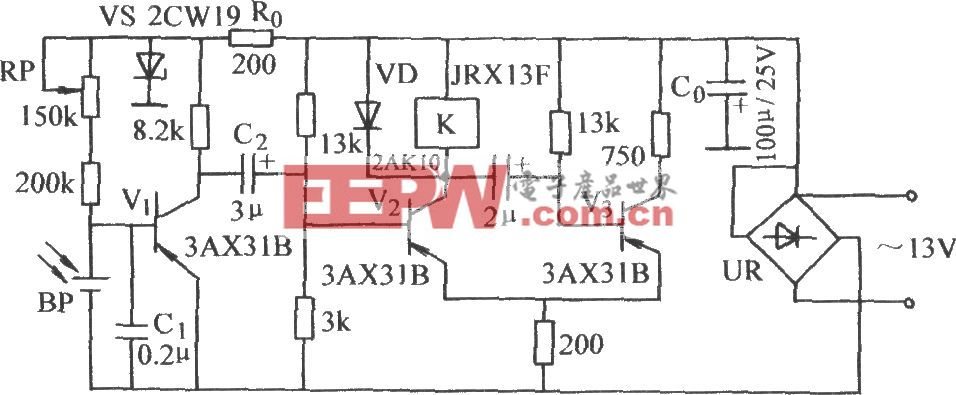
當同時存在多個智能體與環境交互時，整個系統就變成一個多智能體系統（multi-agent system）。每個智能體仍然是遵循著強化學習的目標，也就是是最大化能夠獲得的累積回報，而此時環境全局狀態的改變就和所有智能體的聯合動作（joint action）相關了。因此在智能體策略學習的過程中，需要考慮聯合動作的影響。

1.1 多智能體問題的建模——博弈論基礎

馬爾科夫決策過程拓展到多智能體系統，被定義為馬爾科夫博弈（又稱為隨機博弈，Markov/stochastic game）。當我們對博弈論有一定了解后，能夠借助博弈論來對多智能體強化學習問題進行建模，并更清晰地找到求解問題的方法。

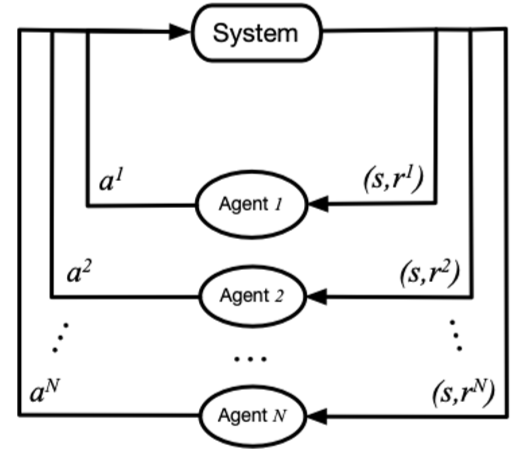
圖 2：馬爾科夫博弈過程。圖源：[2]

在馬爾科夫博弈中，所有智能體根據當前的環境狀態（或者是觀測值）來同時選擇并執行各自的動作，該各自動作帶來的聯合動作影響了環境狀態的轉移和更新，并決定了智能體獲得的獎勵反饋。它可以通過元組 < S,A1,...,An,T,R1,...,Rn > 來表示，其中 S 表示狀態集合，Ai 和 Ri 分別表示智能體 i 的動作集合和獎勵集合，T 表示環境狀態轉移概率，表示損失因子。此時，某個智能體 i 獲得的累積獎勵的期望可以表示為：

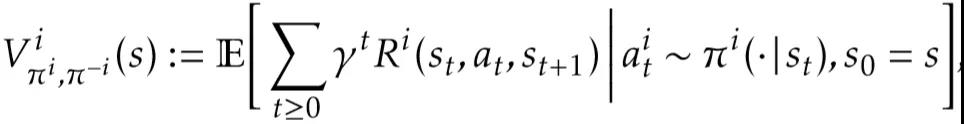
對于馬爾科夫博弈，納什均衡（Nash equilibrium）是一個很重要的概念，它是在多個智能體中達成的一個不動點，對于其中任意一個智能體來說，無法通過采取其他的策略來獲得更高的累積回報，在數學形式上可以表達為：

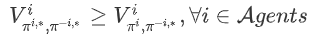
在該式中，π^{i,}表示智能體 i 的納什均衡策略。

值得注意的是，納什均衡不一定是全局最優，但它是在概率上最容易產生的結果，是在學習時較容易收斂到的狀態，特別是如果當前智能體無法知道其他智能體將會采取怎樣的策略。這里舉個簡單的例子來幫助理解，即博弈論中經典的囚徒困境。根據兩個人不同的交代情況，判刑的時間是不一樣的：

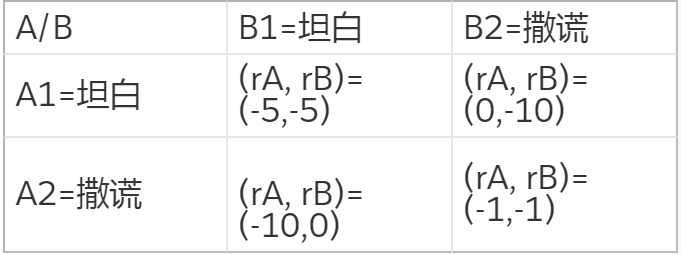
在這個表格中，當 A 和 B 都選擇撒謊時，能夠達到全局最優的回報。但是每個個體都不知道另外的個體會做出怎樣的行為，對于 A 或者是來 B 說，如果改成選擇坦白，則能夠獲得更優的回報。實際上，對于 A 或者 B 來說，此時不管另外的個體選擇了哪種行為，坦白是它能夠獲得最優回報的選擇。所以，最終會收斂到 A 和 B 都選擇坦白，即囚徒困境中的納什均衡策略。

均衡求解方法是多智能體強化學習的基本方法，它對于多智能體學習的問題，結合了強化學習的經典方法（如 Q-learning）和博弈論中的均衡概念，通過 RL 的方法來求解該均衡目標，從而完成多智能體的相關任務。這種思路在后面介紹具體的學習方法中會有所體現。

相比于單智能體系統，強化學習應用在多智能體系統中會遇到哪些問題和挑戰？

1、環境的不穩定性：智能體在做決策的同時，其他智能體也在采取動作；環境狀態的變化與所有智能體的聯合動作相關；

2、智能體獲取信息的局限性：不一定能夠獲得全局的信息，智能體僅能獲取局部的觀測信息，但無法得知其他智能體的觀測信息、動作和獎勵等信息；

3、個體的目標一致性：各智能體的目標可能是最優的全局回報；也可能是各自局部回報的最優；

4、可拓展性：在大規模的多智能體系統中，就會涉及到高維度的狀態空間和動作空間，對于模型表達能力和真實場景中的硬件算力有一定的要求。

1.2 多智能體問題的求解——多智能體強化學習算法介紹

對于多智能體強化學習問題，一種直接的解決思路：將單智能體強化學習方法直接套用在多智能體系統中，即每個智能體把其他智能體都當做環境中的因素，仍然按照單智能體學習的方式、通過與環境的交互來更新策略；這是 independent Q-learning 方法的思想。這種學習方式固然簡單也很容易實現，但忽略了其他智能體也具備決策的能力、所有個體的動作共同影響環境的狀態，使得它很難穩定地學習并達到良好的效果。

在一般情況下，智能體之間可能存在的是競爭關系（非合作關系）、半競爭半合作關系（混合式）或者是完全合作關系，在這些關系模式下，個體需要考慮其他智能體決策行為的影響也是不一樣的。參考綜述[3]，接下來的部分將根據智能體之間的關系，按照完全競爭式、半競爭半合作、完全合作式來闡述多智能體問題的建模以及求解方法。

1.2.1 智能體之間是完全競爭關系

minimax Q-learning 算法用于兩個智能體之間是完全競爭關系的零和隨機博弈。首先是最優值函數的定義：對于智能體 i，它需要考慮在其他智能體（i-）采取的動作（a-）令自己（i）回報最差（min）的情況下，能夠獲得的最大（max）期望回報。該回報可以表示為：

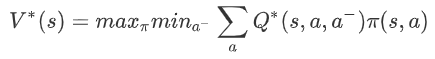
在式子中，V 和 Q 省略了智能體 i 的下標，是因為在零和博弈中設定了 Q1=-Q2，所以上式對于另一個智能體來說是對稱等價的。這個值函數表明，當前智能體在考慮了對手策略的情況下使用貪心選擇。這種方式使得智能體容易收斂到納什均衡策略。在學習過程中，基于強化學習中的 Q-learning 方法，minimax Q-learning 利用上述 minimax 思想定義的值函數、通過迭代更新 Q 值；動作的選擇，則是通過線性規劃來求解當前階段狀態 s 對應的納什均衡策略。

圖 3：minimax-Q learning 算法流程。圖源[4]

minimax Q 方法是競爭式博弈中很經典的一種思想，基于該種思想衍生出很多其他方法，包括 Friend-or-Foe Q-learning、correlated Q-learning，以及接下來將要提到的 Nash Q-learning。

1.2.2 智能體之間是半合作半競爭（混合）關系

雙人零和博弈的更一般形式為多人一般和博弈（general-sum game），此時 minimax Q-learning 方法可擴展為 Nash Q-learning 方法。當每個智能體采用普通的 Q 學習方法，并且都采取貪心的方式、即最大化各自的 Q 值時，這樣的方法容易收斂到納什均衡策略。Nash Q-learning 方法可用于處理以納什均衡為解的多智能體學習問題。它的目標是通過尋找每一個狀態的納什均衡點，從而在學習過程中基于納什均衡策略來更新 Q 值。

具體地，對于一個智能體 i 來說，它的 Nash Q 值定義為：

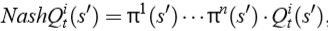
此時，假設了所有智能體從下一時刻開始都采取納什均衡策略，納什策略可以通過二次規劃（僅考慮離散的動作空間，π是各動作的概率分布）來求解。

在 Q 值的迭代更新過程中，使用 Nash Q 值來更新：

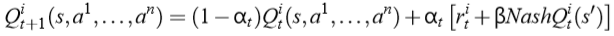
可以看到，對于單個智能體 i，在使用 Nash Q 值進行更新時，它除了需要知道全局狀態 s 和其他智能體的動作 a 以外，還需要知道其他所有智能體在下一狀態對應的納什均衡策略π。進一步地，當前智能體就需要知道其他智能體的 Q(s')值，這通常是根據觀察到的其他智能體的獎勵和動作來猜想和計算。所以，Nash Q-learning 方法對智能體能夠獲取的其他智能體的信息（包括動作、獎勵等）具有較強的假設，在復雜的真實問題中一般不滿足這樣嚴格的條件，方法的適用范圍受限。

圖 4：nash-Q learning 算法流程。圖源：[5]

1.2.3 智能體之間是完全合作關系

前面提到的智能體之間的兩種關系，都涉及到了個體和個體的相互競爭，所以對于個體來說，在策略學習過程中考慮對方（更一般地，其他智能體）的決策行為，才能夠做出更好地應對動作，這是比較容易理解的。那么，如果智能體之間完全是合作關系，個體的決策也要考慮其他智能體的決策情況嗎？實際上，“合作”意味著多個智能體要共同完成一個目標任務，即這個目標的達成與各個體行為組合得到的聯合行為相關；如果個體“一意孤行”，那么它很難配合其他隊友來共同獲得好的回報。所以，智能體的策略學習仍然需要考慮聯合動作效應，要考慮其他具有決策能力的智能體的影響。

怎樣實現在智能體策略學習過程中考慮其他協作智能體的影響呢？這個問題我們可以分類討論，分類的依據是具體問題對于智能體協作的條件要求，即智能體通過協作獲得最優回報時，是否需要協調機制:

1、不需要協作機制

對于一個問題（或者是任務），當所有智能體的聯合最優動作是唯一的時候，完成該任務是不需要協作機制的。這個很容易理解，假設對于環境中的所有智能體 {A,B} 存在不只一個最優聯合動作，即有 {πA,πB} 和{hA,hB}，那么 A 和 B 之間就需要協商機制，決定是同時取π，還是同時取 h；因為如果其中一個取π、另一個取 h，得到的聯合動作就不一定是最優的了。Team Q-learning 是一種適用于不需要協作機制的問題的學習方法，它提出對于單個智能體 i，可以通過下面這個式子來求出它的最優動作 hi：

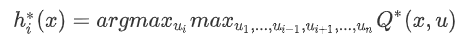
Distributed Q-learning 也是一種適用于不需要協作機制的問題的學習方法，不同于 Team Q-learning 在選取個體最優動作的時候需要知道其他智能體的動作，在該方法中智能體維護的是只依據自身動作所對應的 Q 值，從而得到個體最優動作。

隱式的協作機制

在智能體之間需要相互協商、從而達成最優的聯合動作的問題中，個體之間的相互建模，能夠為智能體的決策提供潛在的協調機制。在聯合動作學習（joint action learner，JAL）[6]方法中，智能體 i 會基于觀察到的其他智能體 j 的歷史動作、對其他智能體 j 的策略進行建模。在頻率最大 Q 值（frequency maximum Q-value, FMQ）[7]方法中，在個體 Q 值的定義中引入了個體動作所在的聯合動作取得最優回報的頻率，從而在學習過程中引導智能體選擇能夠取得最優回報的聯合動作中的自身動作，那么所有智能體的最優動作組合被選擇的概率也會更高。

JAL 和 FMQ 方法的基本思路都是基于均衡求解法，但這類方法通常只能處理小規模（即智能體的數量較少）的多智能體問題：在現實問題中，會涉及到大量智能體之間的交互和相互影響，而一般的均衡求解法受限于計算效率和計算復雜度、很難處理復雜的情況。在大規模多智能體學習問題中，考慮群體聯合動作的效應，包括當前智能體受到的影響以及在群體中發揮的作用，對于智能體的策略學習是有較大幫助的。

基于平均場理論的多智能體強化學習（Mean Field MARL, MFMARL）方法是 UCL 學者在 2018 年 ICML 會議上提出的一種針對大規模群體問題的方法，它將傳統強化學習方法（Q-learning）和平均場理論（mean field theory）相結合。平均場理論適用于對復雜的大規模系統建模，它使用了一種簡化的建模思想：對于其中的某個個體，所有其他個體產生的聯合作用可以用一個 “平均量” 來定義和衡量。此時，對于其中一個個體來說，所有其他個體的影響相當于一個單體對于它的影響，這樣的建模方式能夠有效處理維度空間和計算量龐大的問題。

MFMARL 方法基于平均場理論的建模思想，將所有智能體看作一個“平均場”，個體與其他智能體之間的關系可以描述為個體和平均場之間的相互影響，從而簡化了后續的分析過程。

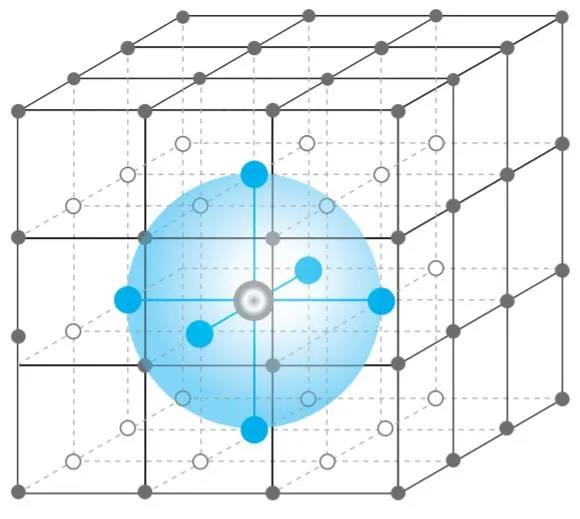
圖 5：基于平均場理論的多智能體建模方式，單個智能體只考慮與相鄰的其他智能體（藍色球體區域）的相互作用。圖源：[8]

首先，為了處理集中式全局值函數的學習效果會受到智能體數量（聯合動作的維度）的影響，對值函數進行分解。對于單個智能體 j，它的值函數 Qj(s,a)包含了與所有 Nj 個相鄰智能體 k 之間的相互作用：

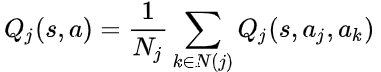
然后，將平均場理論的思想結合到上式中。考慮離散的動作空間，單個智能體的動作采用 one-hot 編碼的方式，即 aj=[h(aj_1), ... h(aj_d)]，其中 h(aj_i)=1 if aj=aj_i ?: 0；其他相鄰智能體的動作可以表示為平均動作 \ bar{aj}和一個波動δ的形式：

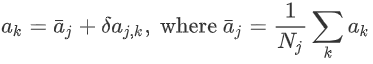
利用泰勒二階展開，得到

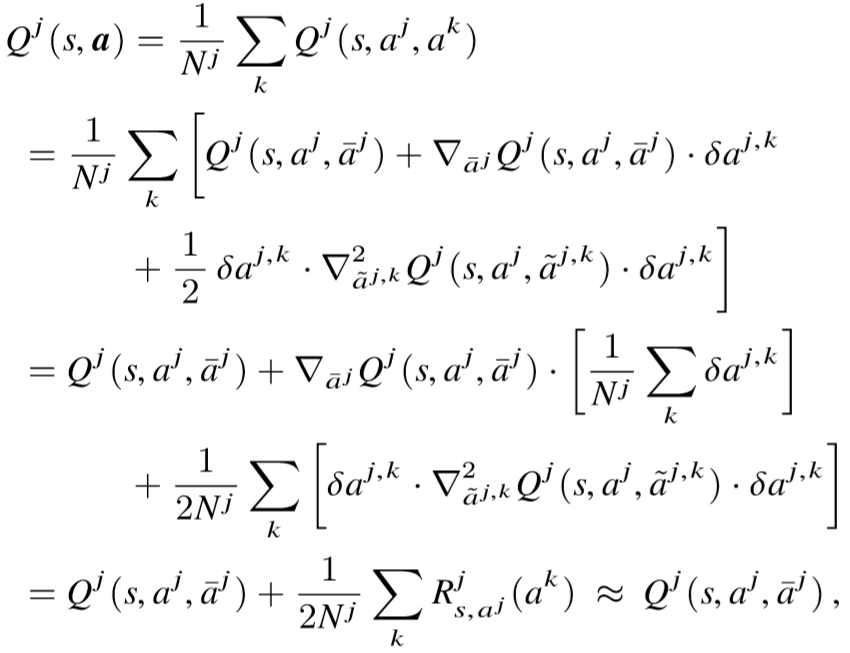
該式子即是將當前智能體 j 與其他相鄰智能體 k 的相互作用，簡化為當前智能體 j 和虛擬智能體 \ bar{j}的相互作用，是平均場思想在數學形式上的體現。此時，在學習過程中，迭代更新的對象為平均場下的 Q(s,aj,\bar{aj})值（即 MF-Q），有：

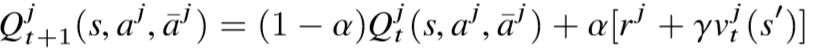
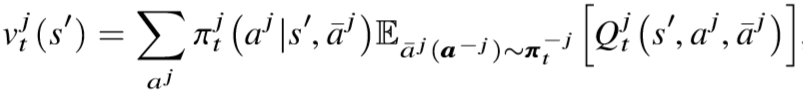
在更新中使用 v 而不是使用 max Q 的原因在于：對 Q 取 max，需要相鄰智能體策略 \ bar{aj}的合作，而對于智能體 j 來說是無法直接干涉其他智能體的決策情況；另一方面，貪心的選擇依舊會導致學習過程受到環境不穩定性的影響。

對應地，智能體 j 的策略也會基于 Q 值迭代更新，使用玻爾茲曼分布有：

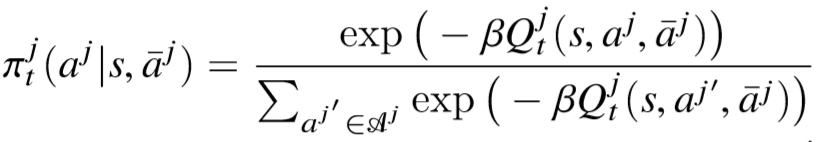
原文證明了通過這樣的迭代更新方式，\bar{aj}最終能夠收斂到唯一平衡點的證明，并推出智能體 j 的策略πj 能夠收斂到納什均衡策略。

2、顯式的協作機制

關于顯式的協作機制，我們將通過多智能體深度強化學習在多機器人領域的應用中會簡單介紹（主要是人機之間的交互，考慮現存的一些約束條件 / 先驗規則等）。

2. 多智能體深度強化學習

隨著深度學習的發展，利用神經網絡的強大表達能力來搭建逼近模型（value approximation）和策略模型（常見于 policy-based 的 DRL 方法）。深度強化學習的方法可以分為基于值函數（value-based）和基于策略（policy-based）兩種，在考慮多智能體問題時，主要的方式是在值函數的定義或者是策略的定義中引入多智能體的相關因素，并設計相應的網絡結構作為值函數模型和策略模型，最終訓練得到的模型能夠適應（直接或者是潛在地學習到智能體相互之間的復雜關系），在具體任務上獲得不錯的效果。

2.1 policy-based 的方法

在完全合作的 setting 下，多智能體整體通常需要最大化全局的期望回報。前面提到一種完全集中式的方式：通過一個中心模塊來完成全局信息的獲取和決策計算，能夠直接地將適用于單智能體的 RL 方法拓展到多智能體系統中。但通常在現實情況中，中心化的控制器（centralized controller）并不一定可行，或者說不一定是比較理想的決策方式。而如果采用完全分布式的方式，每個智能體獨自學習自己的值函數網絡以及策略網絡、不考慮其他智能體對自己的影響，無法很好處理環境的不穩定問題。利用強化學習中 actor-critic 框架的特點，能夠在這兩種極端方式中找到協調的辦法。

1. 多智能體 DDPG 方法（Multi-Agent Deep Deterministic Policy Gradient, MADDPG）

這種方法是在深度確定策略梯度（Deep Deterministic Policy Gradient，DDPG）方法的基礎上、對其中涉及到的 actor-critic 框架進行改進，使用集中式訓練、分布式執行的機制（centralized training and decentralized execution），為解決多智能體問題提供了一種比較通用的思路。

MADDPG 為每個智能體都建立了一個中心化的 critic，它能夠獲取全局信息（包括全局狀態和所有智能體的動作）并給出對應的值函數 Qi(x,a1,...,an)，這在一定程度上能夠緩解多智能體系統環境不穩定的問題。另一方面，每個智能體的 actor 則只需要根據局部的觀測信息作出決策，這能夠實現對多智能體的分布式控制。

在基于 actor-critic 框架的學習過程中，critic 和 actor 的更新方式和 DDPG 類似。對于 critic，它的優化目標為：

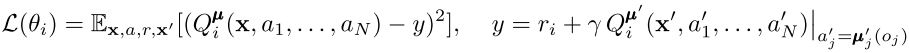
對于 actor，考慮確定性策略μi(ai|oi)，策略更新時的梯度計算可以表示為：

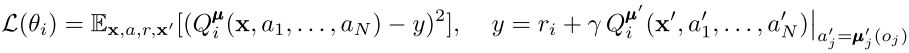
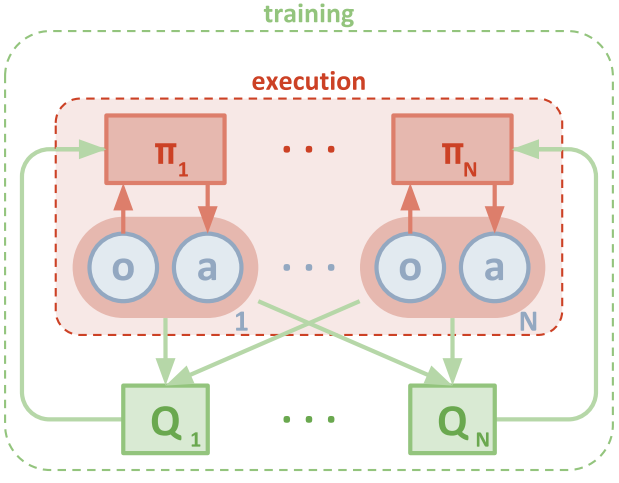
圖 6：中心化的 Q 值學習（綠色）和分布式的策略執行（褐色）。Q 值獲取所有智能體的觀測信息 o 和動作 a，策略π根據個體的觀測信息來輸出個體動作。圖源：[9]

在 MADDPG 中，個體維護的中心化 Q 值需要知道全局的狀態信息和所有智能體的動作信息，此時假設了智能體能夠通過通信或者是某種方式得知其他智能體的觀測值和策略，這種假設前提過于嚴格。MADDPG 進一步提出了可以通過維護策略逼近函數 \ hat{\miu}來估計其他智能體的策略，通過對其他智能體的行為建模使得維護中心化的 Q 值、考慮聯合動作效應對單個個體來說是可行的。智能體 i 在逼近第 j 個智能體的策略函數時，其優化目標是令策略函數能夠近似經驗樣本中智能體 j 的行為，同時考慮該策略的熵，可表示為：

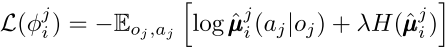
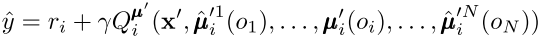
除了考慮聯合動作以外，MADDPG 在處理環境不穩定問題方面還使用了策略集成（policies ensemble）的技巧。由于環境中的每個智能體的策略都在迭代更新，因此很容易出現單個智能體的策略對其他智能體的策略過擬合，即當其他智能體的策略發生改變時，當前得到的最優策略不一定能很好的適應其他智能體的策略。為了緩和過擬合問題，MADDPG 提出了策略集成的思想，即對于單個智能體 i，它的策略μi 是由多個子策略μi^k 構成的集合。在一個 episode 中，只使用一種從集合中采樣得到的子策略進行決策和完成交互。在學習過程中最大化的目標是所有子策略的期望回報，即

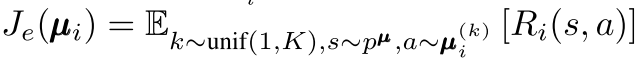
每個子策略的更新梯度為：

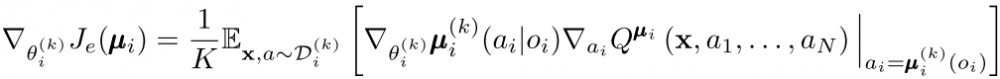
總的來說，MADDPG 的核心是在 DDPG 算法的基礎上，對每個智能體使用全局的 Q 值來更新局部的策略，該方法在完全合作、完全競爭和混合關系的問題中都能取得較好效果。算法流程如下所示：

圖 7：MADDPG 算法流程。圖源：[9]