數字控制式LLC諧振變換器建模分析與驗證

　　通過調節系數K_u使得系統獲較好的低頻增益和穿越頻率點。如圖3所示為補償前后系統的幅頻、相頻增益特性曲線。

　　對比補償前后系統頻域特性，經過補償的系統特性明顯得到了改善，穿越頻率^[4]在11.8kHz處，相位裕度約為87.5o，符合模擬域的環路設計要求。

1.2 數字控制對環路穩定性的影響

　　由于數字控制的離散特性，須將所設計的模擬PID控制器在z域下進行穩定性的判定。作為理想的PID控制器，須滿足以下條件：一是補償后控制系統在z域穩定;二是控制器具有可實現性，本節主要通過z變換實現最優PID參數的整定^[5]。加入補償器后時域控制框圖如圖4所示。

　　分別對功率級傳遞函數G_p(s)、補償器傳遞函數G_c(s)進行z變換，得到其z域的閉環特征方程：

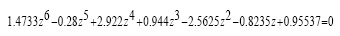(5)

　　從而得到補償后的系統z域閉環零極點分布圖，如圖5所示。

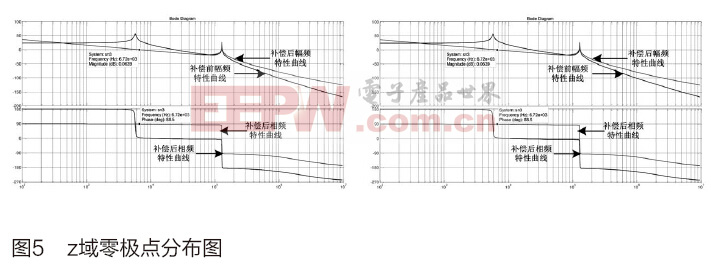
　　根據z域穩定性條件^[6]：閉環傳遞函數的極點應位于單位圓內。可以看出，此時在數字離散域中系統是不穩定的，因此必須選用適合于數字控制的PID控制器設計方法。

　　與傳統的模擬控制器相比，數字控制器由于DSP等數字器件的固有特性，需要在設計時進行相關的考慮。數字控制核心DSP采樣輸出電壓獲得反饋信號，經過補償器控制后作為調制信號^[7]，從而控制輸出電壓恒定，由此可知，更新驅動脈沖的調制信號與實際采樣信號之間存在一個周期的延時，這可以通過加入零階保持器來模擬。并且由于理想采樣開關的存在，使得控制器具有1/Ts的增益特性^[8]，因此可以得到數字PWM在連續時域設計時的等效模型。

　　由上面的介紹可知，與數字PWM相關的延時效應可以通過加入ZOH來等效，實際上，采用數字控制器時，還存在另外一種延時效應，即控制算法的計算延時^[3]，這是由處理器從采樣到輸出一個新的調制量所需要的計算時間決定的，通常假設該控制延時時間為一個調制周期，即Ts，將此延時加入在模擬控制器設計中，可以通過加入延時環節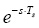來等效，從而得到以下表達式來模擬數字控制帶來的影響。

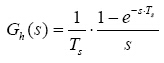(6)

　　通過以上分析，本文以z域穩定性作為設計前提，通過降低系統帶寬解決控制器計算延時等帶來的問題，設計穿越頻率為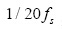，即開關頻率的二十分之一處，保證有足夠的相位裕度。考慮數字影響后，系統開環傳遞函數^[9]為：

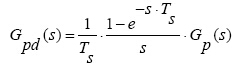(7)

　　將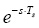用有理函數之和來等效，得到等效后開環傳遞函數：

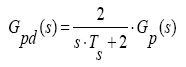(8)

　　得到補償后的開環傳遞函數：

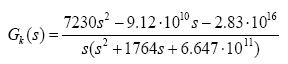(9)

　　在Matlab中繪制補償前后系統開環傳遞函數的Bode圖，如圖6所示。

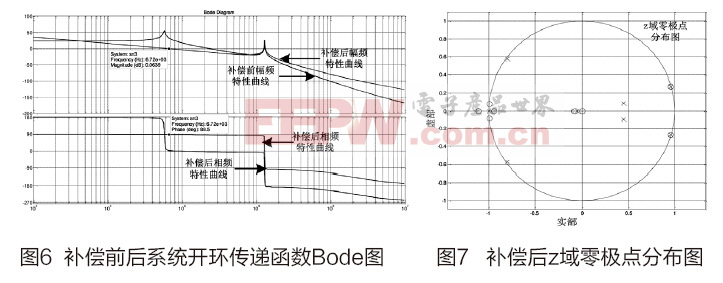
　　如圖6，補償后系統的開環穿越頻率為6.72kHz，相位為88.5°，滿足設計要求。同樣地，仍需對所設計數字補償器進行離散域穩定性的驗證，對補償前開環傳遞函數G_pd(s)以及PID控制器G_cd(s)進行z變換，并乘以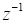得到z域傳遞函數。據此繪制其零極點分布圖如圖7所示。

　　從圖7可以看出，經過重新設計后的PID控制器滿足離散控制要求，所設計的系統是穩定的。