基于旋轉(zhuǎn)體矩量法的天線設(shè)計(jì)
在分析口徑較小,焦距較短,帶有復(fù)雜結(jié)構(gòu)饋源的毫米波反射面天線時(shí),不再適合采用高頻近似方法,而采用全波矩量法求解,由于其巨大的計(jì)算量在PC機(jī)上求解還有很大的困難,提出一種計(jì)算毫米波反射面的新方法,充分利用計(jì)算模型軸對(duì)稱這一幾何特性,建立旋轉(zhuǎn)體矩量法模型,并把該方法應(yīng)用到設(shè)計(jì)微波傳輸系統(tǒng)中的小口徑毫米波反射面天線上。由于在建模中考慮了饋源和主拋物面之間的互耦,計(jì)算結(jié)果和實(shí)驗(yàn)結(jié)果相當(dāng)吻合。通過理論分析和實(shí)驗(yàn),設(shè)計(jì)的口徑為O.3 m天線在整個(gè)角域上滿足了特定的方向圖包絡(luò),達(dá)到了ETSI Class 3的高性能標(biāo)準(zhǔn)。
本文引用地址:http://www.104case.com/article/260959.htm0 引 言
隨著人們對(duì)無(wú)線通信品質(zhì)的需求越來(lái)越高,多層次的通信系統(tǒng)逐步建立起來(lái)。為了使各系統(tǒng)或子系統(tǒng)能夠緊密結(jié)合起來(lái),穩(wěn)定高速率的數(shù)據(jù)傳輸系統(tǒng)是很有必要的。以毫米波天線為基礎(chǔ)的微波傳輸系統(tǒng)由于其成本較低,易于施工等特點(diǎn)受到人們的青睞。該系統(tǒng)要求毫米波天線滿足嚴(yán)格的方向圖包絡(luò)和良好的交叉極化分辨率,一直以來(lái)成為天線設(shè)計(jì)的熱點(diǎn)問題之一。反射面天線的設(shè)計(jì)方法基本上是幾何光學(xué)和物理光學(xué)等高頻近似方法。對(duì)于電大尺寸的反射面天線,用這種方法分析計(jì)算是合理的。對(duì)于口徑較小,饋源結(jié)構(gòu)比較復(fù)雜的反射面天線,高頻方法顯然不適合應(yīng)用。文獻(xiàn)[1]在饋源上采用低頻方法,如矩量法、FDTD等,在反射面天線上則采用高頻方法,計(jì)算在較小的主瓣附近區(qū)域內(nèi)的方向圖,得到比較合理的結(jié)果,但是由于沒有考慮到饋源系統(tǒng)與主反射面互耦等效應(yīng)的影響,對(duì)于大角度區(qū)域,其結(jié)果往往和測(cè)量結(jié)果差別很大。微波傳輸系統(tǒng)要求的微波傳輸天線,經(jīng)常是口徑小,焦距比短的毫米波反射面天線,且在全空間滿足一定的方向圖包絡(luò)要求。由于這類天線不能滿足高頻方法要求的電大尺寸條件,且要求分析方法能對(duì)天線的遠(yuǎn)副瓣和背瓣精確的求解,故而高頻近似方法不能用于該類問題的求解。目前,采用矩量法分析電大尺寸和復(fù)雜結(jié)構(gòu)的研究是計(jì)算電磁學(xué)的熱點(diǎn)問題,特別是文獻(xiàn)[6]采用綜合函數(shù)法與矩量法相結(jié)合,把復(fù)雜結(jié)構(gòu)分為幾塊,對(duì)每塊進(jìn)行依次求解,雖然使矩量法不能求解的問題得到解決,但求解時(shí)間仍然很長(zhǎng)。
本文采用矩量法,充分利用軸對(duì)稱反射面天線的幾何結(jié)構(gòu)這一特性,采用旋轉(zhuǎn)體矩量法(BOR MoM)進(jìn)行求解,使三維問題轉(zhuǎn)化為二維問題。目前,采用旋轉(zhuǎn)體矩量法設(shè)計(jì)小口徑反射面天線得到了重視。文獻(xiàn)[8]采用旋轉(zhuǎn)體矩量法設(shè)計(jì)了小口徑微波天線,設(shè)計(jì)頻率為5 GHz,理論結(jié)果和實(shí)驗(yàn)結(jié)果吻合的很好。本文把旋轉(zhuǎn)體矩量法應(yīng)用到毫米波天線上,這在以往文獻(xiàn)上還比較少。實(shí)驗(yàn)證明,這種方法能夠有效分析具有軸對(duì)稱結(jié)構(gòu)的反射面天線,解決了高性能微波傳輸天線的分析設(shè)計(jì)問題。
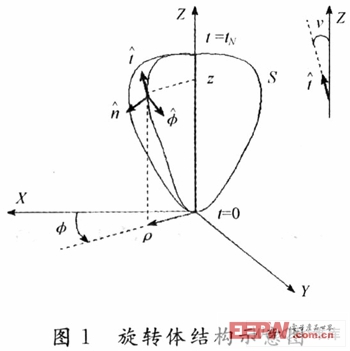
1 旋轉(zhuǎn)體矩量法(BoR MoM)
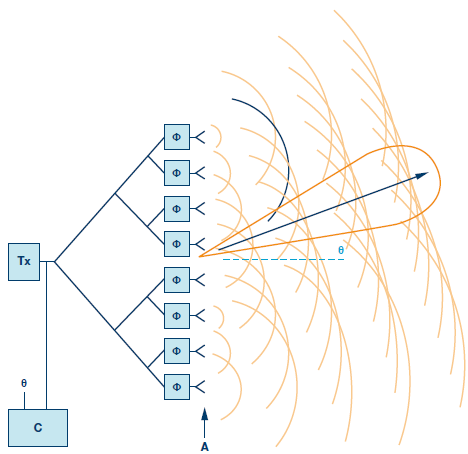
所謂旋轉(zhuǎn)體,是由母線繞旋轉(zhuǎn)軸旋轉(zhuǎn)一周得到的物體,其結(jié)構(gòu)參數(shù)如圖1所示。其中,ρ,φ和z為柱坐標(biāo)的3個(gè)分量;t為母線的長(zhǎng)度;t,φ分別是S上任一點(diǎn)沿t和φ增加的方向;n=φt;v為t和z軸的夾角。對(duì)于散射或輻射問題,經(jīng)常轉(zhuǎn)化為計(jì)算電磁場(chǎng)的邊值問題,采用電場(chǎng)積分方程或磁場(chǎng)積分方程。本文在推導(dǎo)矩陣方程的時(shí)候采用的是電場(chǎng)積分方程。對(duì)于良導(dǎo)體,邊界條件為:
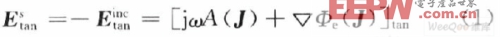
式中:Etan inc是入射電場(chǎng)的切向分量;Etan s為散射電場(chǎng)的切向分量;J為良導(dǎo)體上的感應(yīng)電流。令L算子為:
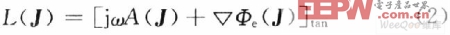
由于所求解
的物體為軸旋轉(zhuǎn)體,則求解電流在φ方向是以2π為周期的周期函數(shù),則用基函數(shù)t'fi(t')和φ'gi(t')展開,可以表示為:
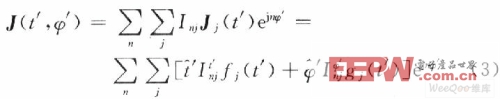

采用咖略金方法,所用與基函數(shù)相同的檢驗(yàn)函數(shù),Wmlt=tfl(t)ejmφ,Wmlφ=φgl(φ)ejmφ,對(duì)式(6)兩邊和檢驗(yàn)函數(shù)求內(nèi)積,得:
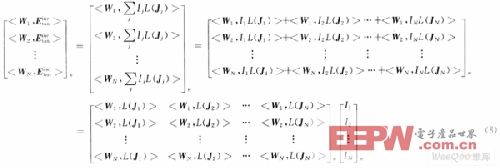
由于傅里葉級(jí)數(shù)的正交性,只有m=n時(shí),式(7)的內(nèi)積不為零。式(7)擴(kuò)展成矩陣的形式則為:
即:








評(píng)論