超聲波瓶體厚度檢測(cè)及其材料分類的研究，保障公共安全

2.3 Restoring（還原）算法簡(jiǎn)介

Restoring算法是一種線性收斂的除法算法。它的主要思想是首先調(diào)整分母并加載分子到余數(shù)寄存器中，然后從余數(shù)中減去調(diào)整的分母并將結(jié)果存在余數(shù)寄存器中，如果新的余數(shù)為正，我們就將商加1，否則商不變并且還需要通過加上分母來還原從前的余數(shù)值。我們可以采用狀態(tài)機(jī)的設(shè)計(jì)結(jié)構(gòu)來實(shí)現(xiàn)該種除法算法思想。

本項(xiàng)目中Restoring算法主要應(yīng)用于：幅度衰減模塊中除法器的設(shè)計(jì)。

2.4 分段函數(shù)算法簡(jiǎn)介

分段函數(shù)是對(duì)于自變量不同的取值范圍，有著不同的對(duì)應(yīng)法則的函數(shù)。對(duì)于分段函數(shù)的實(shí)現(xiàn)具有資源消耗少，處理速度快的特點(diǎn)。例如，一種包含二階非線性函數(shù)的分段函數(shù)，如下式所示：

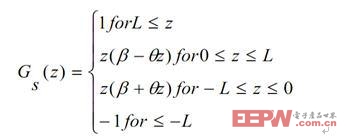
對(duì)于二階非線性函數(shù)的實(shí)現(xiàn)，如圖15 所示：

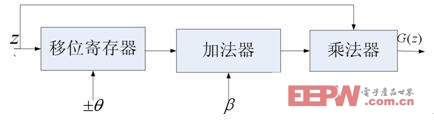
圖15 二階非線性函數(shù)的實(shí)現(xiàn)

本項(xiàng)目中分段函數(shù)主要應(yīng)用于：人工神經(jīng)網(wǎng)絡(luò)中的激活函數(shù)的

f（n）的設(shè)計(jì)。

3. 項(xiàng)目設(shè)計(jì)細(xì)化模塊方案

項(xiàng)目設(shè)計(jì)細(xì)化模塊的框圖，如圖16所示：

本次項(xiàng)目的設(shè)計(jì)難點(diǎn)：

（1）準(zhǔn)確測(cè)定延時(shí)信息的自相關(guān)模塊的設(shè)計(jì)，因?yàn)樽韵嚓P(guān)信息會(huì)對(duì)收發(fā)信號(hào)的幅度提取有著很大的影響。

（2）高效的64階濾波器的設(shè)計(jì)，旨在設(shè)計(jì)一種既節(jié)省硬件資源又能高效實(shí)時(shí)輸出的一種低通濾波器。

（3）可準(zhǔn)確分類的人工神經(jīng)網(wǎng)絡(luò)的設(shè)計(jì)，需要大量的離散學(xué)習(xí)和確定一種準(zhǔn)確的拓?fù)浣Y(jié)構(gòu)。

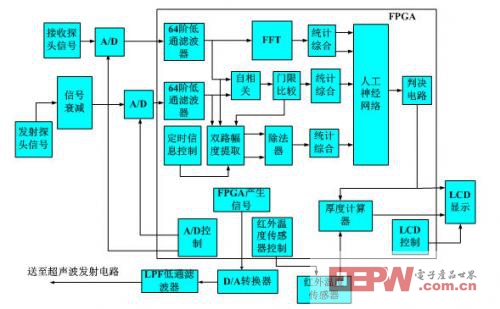
圖16 項(xiàng)目設(shè)計(jì)細(xì)化模塊框圖

推薦閱讀：30例經(jīng)典檢測(cè)、監(jiān)測(cè)、監(jiān)控系統(tǒng)完整解決方案，從實(shí)際應(yīng)用需求出發(fā)